Выплавка чугуна и стали в бывшем советском союзе за 1970 — 1975 гг., тыс. Руб.

	1970 г.	1971 г.	1972 г.	1973 г.	1974 г.	1975 г.
Чугун Сталь	85933 115889	89256 120660	92327 125592	95933 131481	99868 136230	102968 141344

2. Сопоставимость уровней ряда — основная предпосылка анализа рядов динамики

Анализировать ряды динамики нельзя, если приводятся несо­поставимые данные. Проблема сопоставимости данных особенно остро стоит в рядах динамики, потому что они могут охваты­вать значительные периоды времени, за которые могли произойти из­менения, приводящие к не­со­поставимости статистических дан­ных. Несопоставимость статистических данных во времени мо­жет быть обусловлена разными причинами. Важнейшие из них такие: территориальные из­мене­ния, изменение единицы счета, изменение курса валюты, различная степень охвата явления стати­стическими наблюдениями, несовершенство методологии статистического на­блюдения.

Смыкание рядов динамики. Иногда для того, чтобы привести уровни в ряду динамики к со­поставимому и, следовательно, год­ному для анализа виду, приходится прибегать к приему, кото­рый носит название смыкания рядов динамики. Это бывает в том слу­чае, когда вначале мы имеем уровни ряда, исчисленные по одной методологии или в одних границах, А ЗАТЕМ УРОВНИ, ис­численные по другой методологии или в других границах. При этом для того, чтобы произвести смыкание этих двух рядов в один, необходимо, что бы для переходного звена имелись уровни, ис­численные по разной методологии (границах).

Предположим, имеют­ся следующие данные о розничном товарообороте области, где в 1975 г. были изменены границы.

Таблица 10.3

Розничный товарооборот области, млн. грн.

Товарооборот области	1974 г.	1975 г.	1976 г.	1977 г.
В старых границах В новых границах	6700	6900 7500	- 7800	- 8200
Сопоставимый ряд	7283	7500	7800	8200

Чтобы сомкнуть эти два ряда (в старых и новых границах), нужно пересчитать данные за 1974 г. с учетом новых границ, используя для этого цифры 1975 г., где розничный товарооборот дан и в старых, и в новых границах. Исчислим для 1975 г. отноше­ние розничного товарооборота в новых границах к розничному товарообороту в старых границах: 7500 / 6900 = 1.087.

Умножая на этот коэффициент данные за предыдущие годы (в нашем примере 1974 г.), при­ве­денные в старых границах, пере­ведем их в новые границы (для 1974 г.: 6700 • 1,087 = 7283). Сомкнутый сопоставимый ряд динамики приведен в третьей стро­чке таблицы.

3. Показатели анализа динамики

Начальный, конечный и средний уровень ряда. Анализу под­вергаются уровни ряда дина­мики. Различают начальный уровень (у₁), показывающий величину первого члена ряда, ко­нечный уро­вень (у_n), показывающий величину последнего члена ряда, и сред­ний уровень ряда (у-), кото­рый рассчитывается по средней хроно­логической.

Средней хронологической называется средняя, исчисленная из показателей, изменяющихся во времени. Такие средние обобщают хронологическую вариацию.

Расчет среднего уровня в интервальном ряду динамики. Ме­тоды расчета среднего уровня в интервальных и моментных рядах динамики различны. В интервальном ряду, если все интер­валы равны, средний уровень ряда исчисляется по простой средней арифметической: ряда,

где  — сумма уровней ряда; n —их число.

В табл. 10.2 были приведены данные о выплавке чугуна и стали за 1970—1975 гг. По этим данным сделаем расчет среднегодового уровня выплавки чугуна:

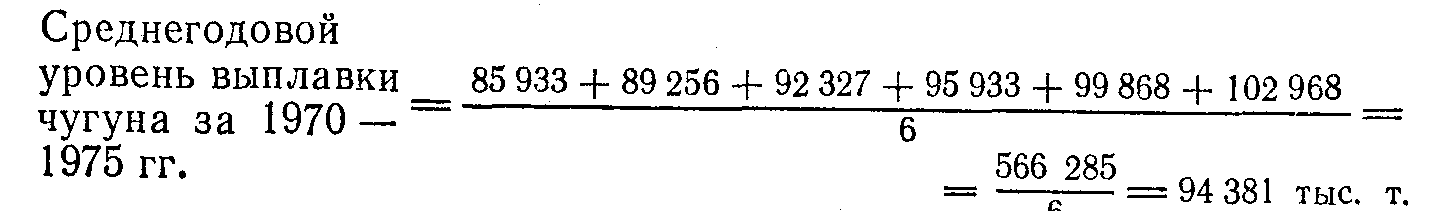
Сложив шесть годовых уровней, мы получили выплавку чугуна за шесть лет 566 285 тыс. т., а разделив эту величину на шесть, узнаем, сколько чугуна выплавляли за 1970—1975 гг. еже­годно в среднем.

Можно изменить единицу расчета и за тот же период исчислить среднемесячный уровень ряда. Для этого 566285 тыс. т нужно разделить не на 6, а на 72 (число месяцев за 6 лет). Мы полу­чим:

Среднемесячный уровень выплавки чугуна за 1970-1975 гг.= 566285 865 / 72 = 7865 тыс. т.

Расчет среднего уровня интерваль­ного ряда динамики требует предварительного суммиро­вания уров­ней ряда. Это суммирование означает укрупнение интервала ряда, которое иногда имеет са­мостоятельные значения для анализа динамики. Приведем пример.

Возьмем интервальный ряд динамики ежедневных данных о сварке труб газопровода на од­ном из крупных строительств.

Таблица 10.4