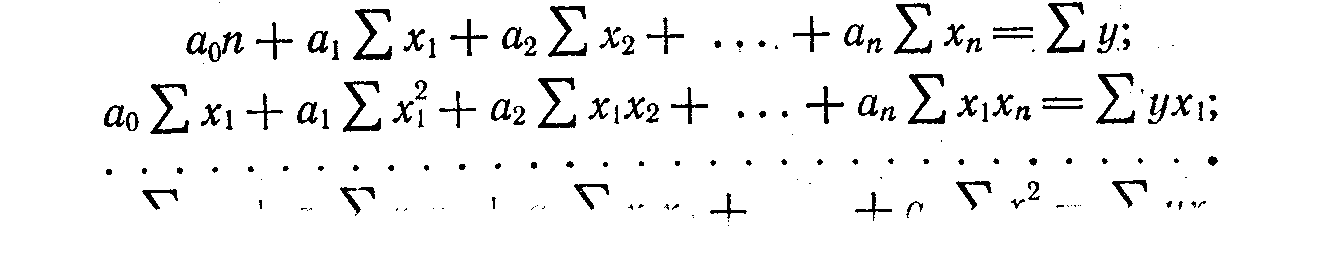10. Многофакторный корреляционно-регрессионный анализ 1

Как известно, явления общественной жизни складываются под воздействием не одного, а целого ряда факторов, т. е. эти явления многофакторны. Между факторами существуют слож­ные взаимосвязи, поэтому их влияние комплексное и его нельзя рассматривать как простую сумму изолированных влияний.

Многофакторный корреляционно-регрессионный анализ позволяет оценить меру влияния на исследуемый результативный показатель каждого из включенных в модель (уравнение) факто­ров при фиксированном положении (на среднем уровне) остальные факторов, а также при лю­бых возможных сочетаниях факторов с определенной степенью точности найти теоретическое значение этого показателя. При этом важным условием является отсутствие между факторами функциональной связи.

Математически задача формулируется следующим образом. Требуется найти аналитическое выражение, наилучшим образов отражающее связь факторных признаков с результативным, т. е найти функцию

Задача состоит в том, чтобы раскрыть характер и степень влияния аргументов на функцию. Решение этой задачи позволяет раскрыть механизм управления величиной изучаемого показа­теля, что имеет большое практическое значение, например, для оценки результа­тов работы предприятия, выявления его объективных возможно­стей и вскрытия резервов роста эффектив­ности производства.

Наиболее сложной проблемой представляется выбор формы связи.

Поэто­му, принимая во внимание, что в большинстве практических случаев любую функцию многих переменных путем логарифмирования или замены переменных можно свести к линей­ному виду, уравнение множественной регрессии можно строить в линейной форме:

С помощью многофакторного корреляционного анализа нахо­дятся различного рода харак­теристики тесноты связи между изу­чаемым показателем и факторами: парные, частные и мно­жествен­ные коэффициенты корреляции, множественный коэффициент де­терминации.

Парные коэффициенты корреляции. Для измерения тесноты связи между двумя из рас­сматриваемых переменных (без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициен­тов и их интерпретация аналогичны линейному коэффициенту кор­реляции в случае однофакторной связи.

Частные коэффициенты корреляции. Однако в реальных усло­виях все переменные, как правило, взаимосвязаны. Теснота этой связи определяется частными коэффициентами корреля­ции, которые характеризуют степень влияния одного из аргументов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне. В зависимости от количества переменных, влияние которых исключается (элиминируется), частные коэффи­ци­енты корреляции могут быть различного порядка.

Частный коэффициент корреляции первого порядка между при­знаками у и х₁ при исклю­ченном влиянии признака х₂ вычисляется по формуле

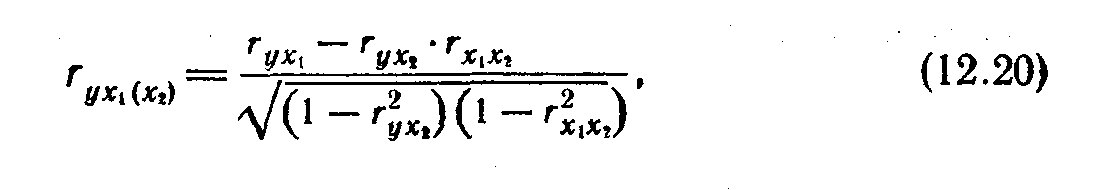
где r — парные коэффициенты корреляции между соответствую­щими признаками.

Совокупный коэффициент множественной корреляции. Показа­телем тесноты связи, ус­танавливаемой между результативным и двумя или более факторными признаками, является со­вокупный коэффициент множественной корреляции R. Он служит основным показателем ли­нейной корреляционной связи. В случае линейной двухфакторной связи совокупный коэффици­ент множественной кор­реляции может быть рассчитан по формуле

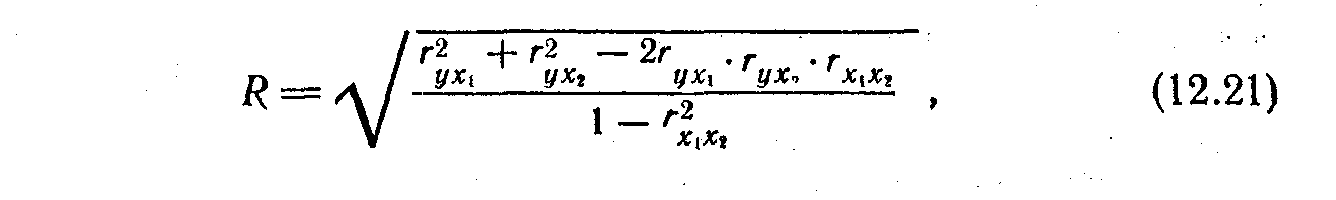
где r — линейные коэффициенты корреляции (парные), а подстроч­ные индексы показы­вают, между какими признаками они ис­числяются.

Совокупный коэффициент множественной корреляции измеряет одновременное влияние факторных признаков на результативный. Его значения находятся в пределах от 0 до 1. Чем меньше наблю­даемые значения изучаемого показателя отклоняются от линии множественной регрессии, тем корреляционная связь является бо­лее интенсивной, а следовательно, величина R. ближе к единице.

Совокупный коэффициент множественной детерминации. Вели­чина R² называется со­вокупным коэффициентом множественной детерминации. Она показывает, какая доля вариации изучаемого показателя объясняется влиянием факторов, включенных в урав­нение множествен­ной регрессии. Значения совокупного коэффи­циента множественной детерминации находятся в пределах от 0 до 1. Поэтому, чем R² ближе к единице, тем вариация изучаемого показателя в большей мере характеризуется влиянием отобранных факторов.

Задачей многофакторного регрессионного анализа является по­строение уравнения множест­венной регрессии и нахождение не­известных параметров a_о, a₁, .... а_n, выбранной функции. Пара­метры уравнения, как и в случае парной регрессии, находятся по способу наименьших квадра­тов.

Так, для расчета параметров простейшего уравнения множест­венной регрессии — линейной двухфакторной регрессии

ух = а₀ + а₁х₁ + а₂х₂ (12.22)

Задача. Требуется выявить зависимость производительности труда — у (тыс. грн.) на одно­типных предприятиях—льнозаводах от двух факторов: мощности завода — х₁ ( (тыс. т) и каче­ства обрабатываемого сырья - х₂ (сортономер) при следующей статистической связи между при­знаками:

Таблица 12.18

Корреляционная связь между производительностью труда, мощностью завода и качеством сырья и расчетные данные

№ п/п	Исходные ранние			Расчетные значения
	у	х1	х2	у2	х12	х22	ух1	ух2	х1х2	ух	у-ух	(у-ух)2
1	10,1	13,1	0,82	102,01	171,61	0,67	132,31	8,28	10,74	10,57	-0,47	0.22
2	11,5	13,0	0,86	132,25	169,0	0,74	149,50	9,89	11,18	10,73	+0,77	0,59
3	11,9	14,3	0,90	141,61	204,49	0,81	170,17	10,71	12,87	12,59	-0,69	0,48
4	12,4	13.2	1,10	153,76	174,24	1,21	163,68	13,64	14,52	12,66	—0,26	0,07
5	13,5	14,4	1,00	182,25	207,36	1,00	194,40	13,50	14,40	13,41	+0,09	0,01
6	15,0	15,3	1,20	225,0	231,09	1,44	229,50	18,00	18,36	15,90	—0,90	0,81
7	16,3	15,0	1,10	265,69	225,0	1,21	244,50	17,93	16,50	14,84	+0,16	0,03
	90,7	98,3	6,98	1202,67	1385,79	7,08	1284,06	91,95	98,57	90,70	—	2,21

Подстрочные знаки показывают, между какими признаками исчисляются эти коэффици­енты.

Высокие значения парных коэффициентов корреляции свидетельствуют о сильном влиянии (в отдельности, изолированно) мощности завода и качества сырья на производительность труда.

На основании парных коэффициентов корреляции могут быть рассчитаны частные коэффи­циенты корреляции первого порядка:

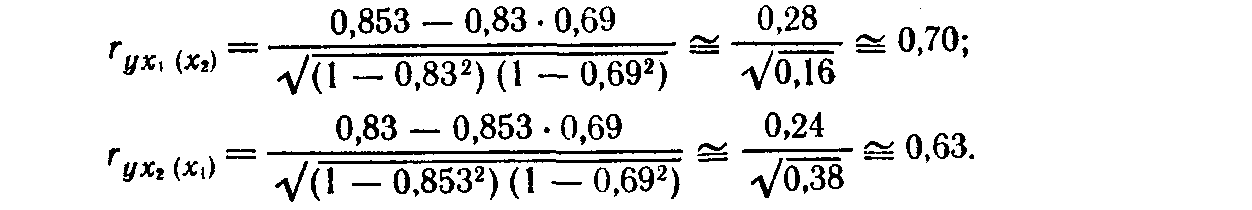
Видим, что связь каждого фактора с изучаемым показателем при условии комп­лексного взаимодействия факторов несколько слабее, но достаточно тесная. Для выявления тесноты связи результативного показателя с обоими факторами одно­временно исчислим совокупный коэффи­циент множественной корреляции R:

Связь достаточно тесная. Совокупный коэффициент множественной детермина­ции R² = 0,839 показывает, что вариация производительности труда на 83,9 % обусловливается двумя факторами. Значит, выбранные факторы существенно влияют на показатель производительно­сти труда. Таким образом, изученная с помощью многофакторного корреляционного анализа статистическая связь меж­ду исследуемыми показателями свидетельствует о целесообразности построения двухфакторной регрессионной модели (уравнения) производительности труда в виде

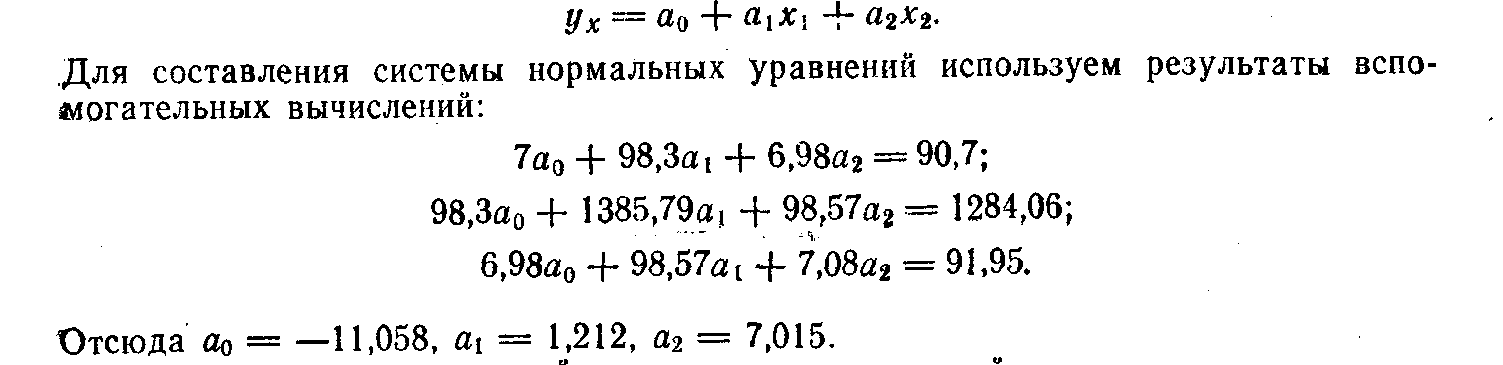
Уравнение множественной регрессии, выражающей зависимость производи­тельности труда у от мощности завода х₁ и качества сырья х₂, примет вид у_х = — 11,058 + 1,212х₁ + 7,015х₂. Вы­числим по нему теоретическую произво­дительность труда ух и занесем данные в таблицу (12.16). Анализ коэффициен­тов уравнения множественной регрессии позволяет сделать вывод о степени влияния каждого из двух факторов на показатель производительности труда. Так, с уве­личением мощности завода на 1 тыс. т льноволокна в год следует ожидать, что производитель­ность труда (выработка продукции на 1 работаю­щего) может вырасти на 1212 грн.; с улучше­нием качества обрабатываемого сырья на 0,1 сортономера — на 701,5 грн.

При этом следует иметь в виду, что между факторными признаками и результативными связь будет прямолинейной лишь в определенных пределах изменения признаков-факторов. Так, производительность труда равномерно по­вышается с увеличением мощности предприятия, но когда мощность достигнет оптимальных размеров, ее повышение постепенно замедляется, а затем может прекратиться и даже смениться снижением. Отсюда можно сделать соответст­вую­щие практические выводы.

Однако коэффициенты регрессии не могут сами по себе опреде­лить, какие из них оказы­вают наибольшее влияние на исследуемый показатель (поскольку они измерены различными единицами), а также в развитии каких факторов заложены крупные резервы его улучшения (так как не учитывается вариация факторов).

Для этого должны быть вычислены частные коэффициенты эластичности (Э_i) и так назы­ваемые _I (вета-коэффициенты).

Различия в единицах измерения факторов устраняются по­мощью частных коэффициентов эластичности, которые рассчитываются по формуле

где а_i — коэффициент регрессии при i-м факторе;

х-_i — среднее значение i - го фактора;

y_i — среднее значение изучаемого показателя.

Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменя­ется, анализируемый показатель изменением на 1 % каждого фактора при фиксированном по­ложении других факторов.

Для определения факторов, в развитии которых заложены и более крупные резервы улуч­шения (с точки зрения целей исследования) изучаемого показателя, необходимо учесть различия степёни варьирования вошедших в уравнение факторов. Это много сделать с помощью _i -ко­эффициентов, которые вычисляютсяя по формуле

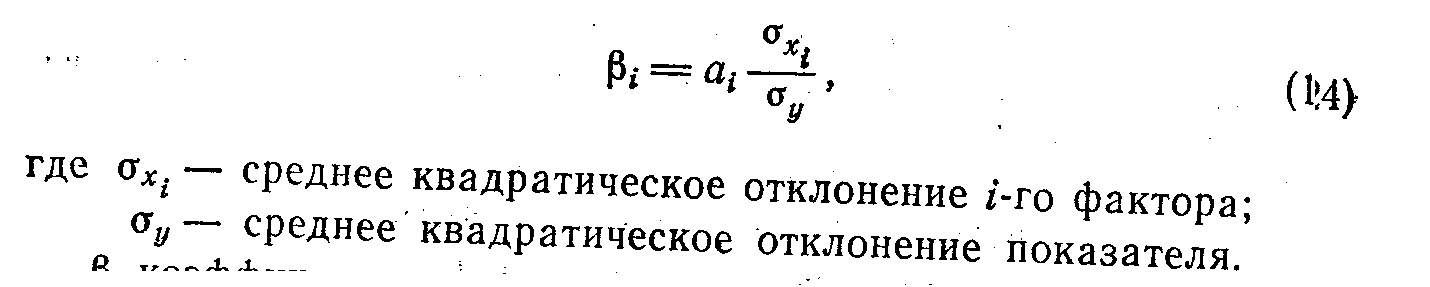
_i - коэффициент показывает, на какую часть среднего квадратического отклонения изменяется результативный признак с изме­няем соответствующего факторного признака на величину его среднего квадратического отклонения.

Рассчитаем коэффициенты эластичности и _i - коэффициенты для наго примера и дадим им экономическую интерпретацию:

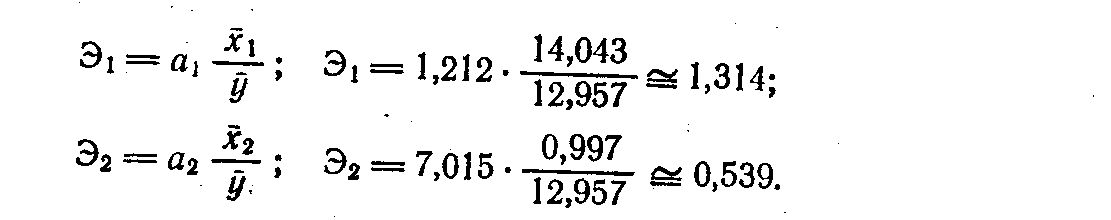
Анализ частных коэффициентов эластичности показывает, что по абсолютному приросту наибольшее влияние на производительность труда оказывает фактор х₁ — мощность завода: увеличение мощности на 1 % дает прирост, производительности труда на 1,31 %. Улучшение на 1 % качества обрабатывает сырья приводит к повышению производительности труда только на 0,54 %.

Для расчета коэффициентов вначале необходимо исчислить среднее квадратичёское откло­нение величин х₁, х₂, у:

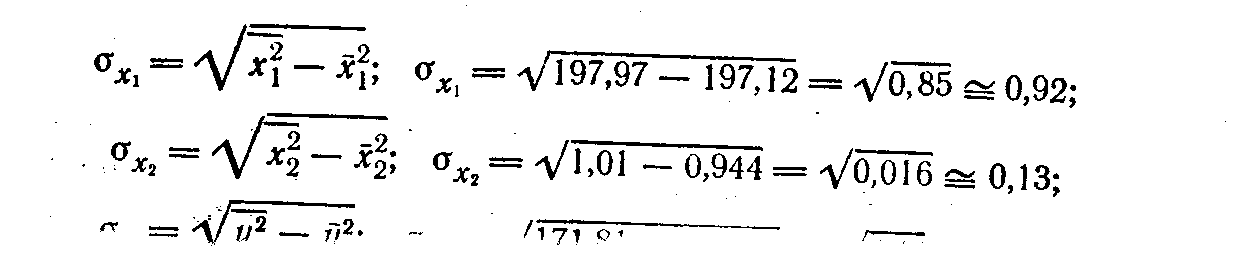
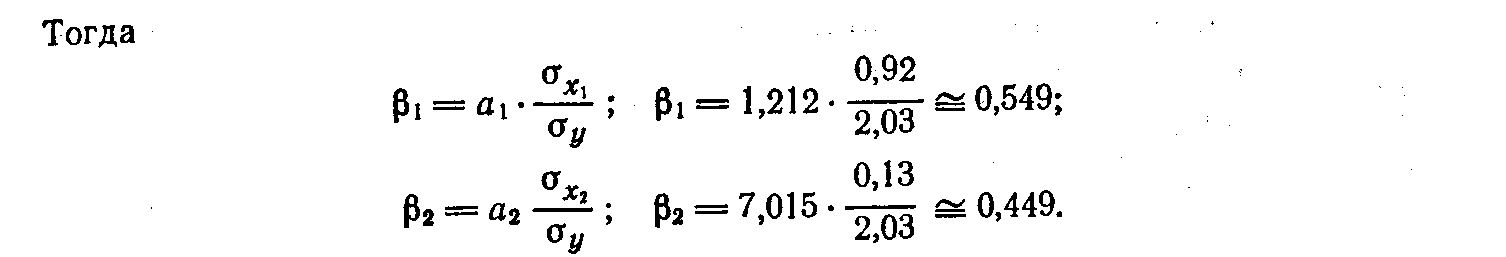
Анализ _i - коэффициентов показывает, что на производительность труда наи­большее влия­ние из двух исследуемых факторов с учетом уровня их колеблемо­сти способен оказать фактор х₁ — мощность завода, так как ему соответствует наибольшее (по абсолютной величине) значе­ние _i -коэффициента.

Таким образом, на основании частных коэффициентов эластич­ности (Э_i) и _i - коэффициен­тов можно судить о резервах предприя­тия, которые заложены в том или ином факторе.

В целях осуществления более глубокого экономического ана­лиза хозяйственной деятельно­сти предприятия необходимо выпол­нить построение многофакторных регрессионных моделей всех основных показателей экономической эффективности: производи­тельности труда, фондо­отдачи, материалоемкости, себестоимости, рентабельности и др.

Увеличение числа существенных факторов, включаемых в мо­дель исследуемого показателя, позволяет выявить дополнительные резервы производства.

Для этого могут быть использованы трехфакторные, четырех­факторные и т. д. уравнения регрессии.

В случае линейной трехфакторной связи уравнение регрессии имеет вид

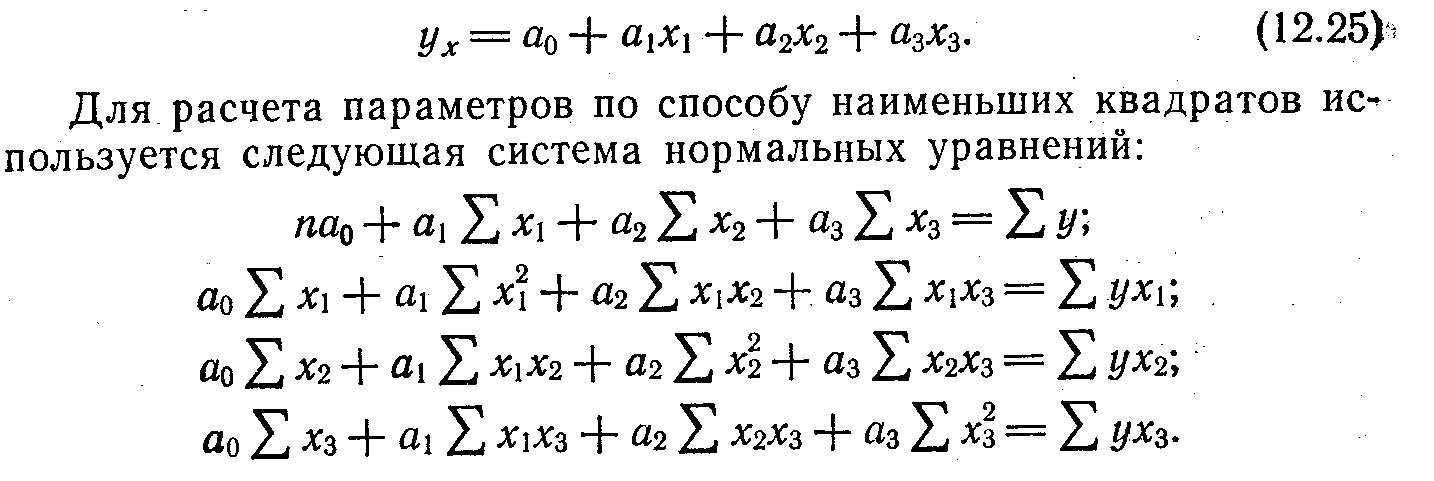
Чтобы получить эту систему, необходимо иметь таблицу зна­чений следующих показателей: х₁, х₂, х₃, у, х²₁, х²₂, х²₃, у², ух₁, ух₂, ух₃, х₁х₂, х₁х₃, х₂х₃.

Для решения уравнения множественной регрессии с n факто­рами у_х = а_о + а₁х₁ + а₂х₂ + • • • ,+ а_nх_n система нормальных урав­нений такова: