8. Однофакторный корреляционно-регрессионный анализ

Корреляционно-регрессионный анализ заключается в построе­нии и анализе статистической модели в виде уравнения регрессии (уравнения корреляционной связи), приближенно выражаю­щей зависимость результативного признака от одного или нескольких признаков-факторов. Пер­воначально рассмотрим однофакторную регрессию. Одной из основных проблем, которую при­хо­дится ре­шать, прежде чем приступить к построению уравнения, является выбор типа функ­ции.

Нахождение теоретической формы связи. Если мы на корреля­ционном поле в нашем при­мере (см. рис. 12.1) соединим точки отрезками прямой, то получим ломаную линию с некоторой тен­денцией к росту (рис. 12.3). Это будет эмпирическая ломаная ли­ния регрессии.

Изломы этой линии свидетельствуют о влиянии на признак у прочих факторов, помимо при­знака х. Чтобы отвлечься (абстраги­роваться) от влияния прочих факторов, нужно прибег­нуть к вы­равниванию полученной ломаной линии регрессии, к нахождению переменных сред­них (у_х) исчисленных в предположении функ­циональной зависимости у от х.

Мы знаем, что в зависимости от харак­тера изменения у с изменением х связи могут быть линейными и нелинейными.

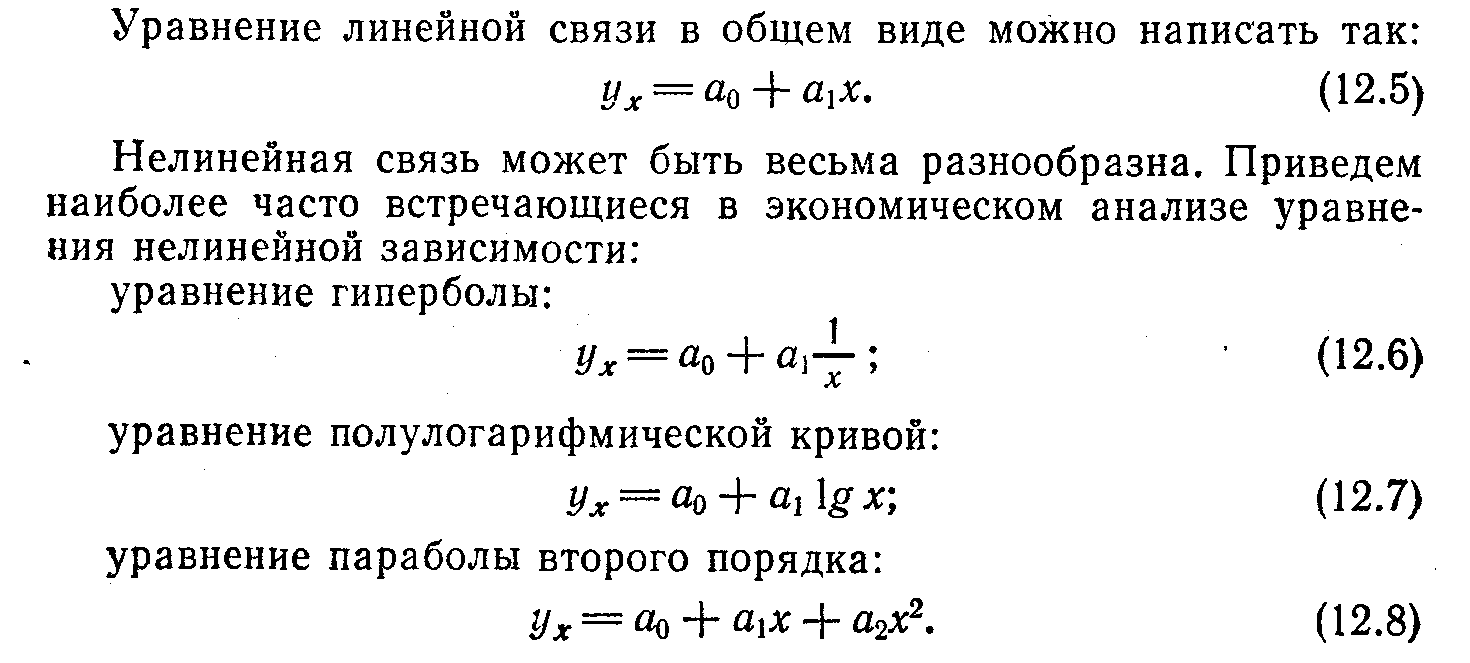
Выбор теоретической формы связи всегда связан с некоторой условностью.

Эта тео­ретическая линия связи иначе называется линией регрессии, а ее поиск, построение, анализ и практическое применение — регрессионным анализом.

Выравнивание по прямой. Уравнение прямой в общем виде: у_х = а_о + а₁х. Найти теорети­ческое уравнение связи — зна­чит в данном случае определить па­раметры прямой. Эти пара­метры находят способом наимень­ших квадратов, который дает следующую систему нормаль­ных урав­нений для нахождения пара­метров прямой:

Таблица 12.11

Выравнивание по прямой

№ п/п	х	у	х2	ху	ух	у - ух	(у - ух)2
1	6,0	2	36,00	12,0	2,9	—0,9	0,81
2	6,1	3	37,21	18,3	3.0	0	0
3	6,8	6	46,24	40,8	3,6	2,4	5,76.
4	7,2	4	51,84	28,8	3,9	0,1	0,01
5	7,4	2	54,76	14,8	4,1	-2,1	4,41
6	7,9	3	62,41	23,7	4,5	-1,5	2,25.
7	8,2	4	67,24	32,8	4,8	—0,8	0,64
8	8,5	5	72,25	42,5	5,0	0	0
9	8,9	6	79,21	53,4	5,4	0,6	0,36
10	9,1	8	82,81	72,8	5,5	2,5	6,25
11	9,4	5	88,36	47,0	5,8	—0,8	0,64
12	9,9	7	98,01	69,3	6,2	0,8	0,64
13	10,5	7	110,25	73,5	6,7	0,3	0,09
14	11.2	8	125,44	89,6	7,3	0,7	0,49
15	11,3	6	127,69	67,8	7,4	—1,4	1,96
16	11,5	9	132,25	103,5	7,6	1,4	1,96
17	11,7	9	136,89	105,3	7,8	1.2	1,44
18	12,1	8	146,41	96,8	8,1	-0,1	0,01
19	12,3	7	151,29	86,1	8,3	—1,3	1,6»
20	12,6	8	158,76	100,8	8,5	—0,5	0,25
21	12,7	9	161,29	114,3	8,6	0,4	0,16
22	12,9	6	166,41	77,4	8,8	-2,8	7,84
23	13,0	10	169,00	130,0	8,9	1,1	1,21
24	13,2	9	174,24	118,8	9,1	-0,1	0,01
25	13,3	10	176,89	133,0	9,2	0,8	0,64
Итого	253,7	161	2713,25	1753,1	161	- 12,3 +12,3	39,52

регрессии выражает функциональную зависимость у от х.

Этот параметр, который называ­ется коэффициентом рег­рессии, характеризует, в какой мере уве­личивается у_х с ростом величины х. В нашем примере прирост энерговооруженности труда на 1 тыс. кВт-ч в году на одного ра­ботающего дает прирост производительности труда на 860 шт. из­делий в год на одного работающего.

Коэф­фициент эластичности характе­ризует, на сколько процентов увеличивается ух при увеличе­нии х на один процент и рассчитывается по формуле

В нашем примере коэффициент эластичности на первом предприятии при х = 6,0 будет рав­няться: 0,86 * (6 / 2,9) = 1,78. Следовательно, на 1 % прироста энерговооруженности труда его производитель­ность возрастет на 1,78 %.

Индекс корреляции (теоретическое корреляционное отношение - самостоят. Изуч. ре­ферат).

Линейный коэффициент корреляции. Частным случаем общего индекса корреляции явля­ется линейный коэффициент корреляции, применение которого ограничено только линейной фор­мой связи (у_х = а_о + а₁х).

Дальнейшее преобразование приводит формулу к следующему виду, наиболее удобному для вычислений:

В отличие от корреляционного отношения и индекса корреляции коэффициент корреляции показывает не только тесноту, но и на­правление связи. Его значение изменяется от — 1 до +1. Если коэф­фициент корреляции имеет знак минус, значит, связь обратная, если имеет знак плюс, связь прямая. Близость к единице в том и другом случае характеризует близость к функцио­нальной за­висимости.

Из приведенной формулы коэффициента корреляции (12.8) можно определить коэффициент регрессии, не исчисляя уравнения связи. Коэффициент регрессии (01) равняется:

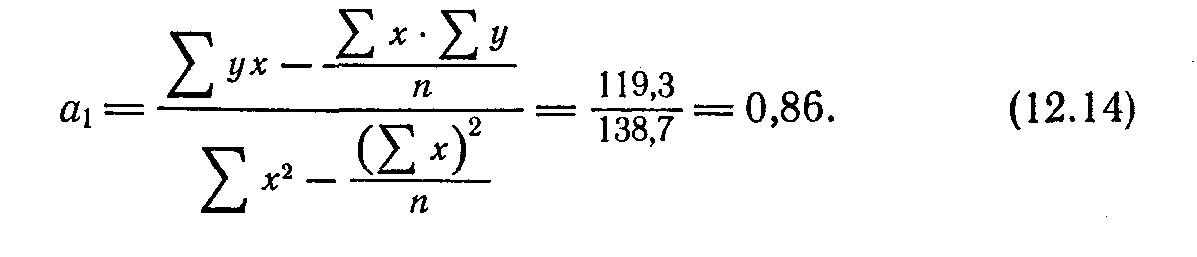
Проверка значимости корреляционной связи с помощью диспер­сионного анализа.

9. Нелинейные зависимости

Выравнивание по гиперболе. Рассмотрим, например, связь между уровнем издержек об­ращения (процент их суммы к товаро­обороту) в магазинах и размером их товарооборота. Связь эта обратная: с увеличением товарооборота уменьшается уровень издержек. В этом проявляется преимущество крупного предприя­тия. Однако размер снижения непостоянный: он более быст­рый вначале на мелких предприятиях и существенно замедляется на предприятиях средних и крупных. Это происходит потому, что в составе издержек обращения имеются два вида расхо­дов. Один вид расходов — это расходы, сумма которых возрастает пример­но пропорционально росту товарооборота, например транспортные расходы, заработная плата, выплачиваемая в про­центах к товаро­обороту, и т. д. Эти расходы по своему уровню остаются неизмен­ными с ростом товарооборота (обозначим их уровень через а_о). Расходы другого вида (как, например, расходы на помещение и административные расходы), возрастают в сумме медленнее, чем растет това­рооборот, и уровень их снижается. Обозначим сумму этих расходов через а₁, а уровень—через а₁ / х. Тогда теоретическая форма зависимости уровня издержек обращения от размера товаро­оборота при условии функциональной связи определится я виде уравнения гиперболы:

Покажем выравнивание по гиперболе на примере анализа за­висимости уровня издержек об­ращения от размера товарооборота у 10 магазинов (табл. 12.13).

Таблица 12.13

Выравнивание по гиперболе

№ п/п	Товарооборот, тыс. грн. (х)	Уровень издержек обращения (у)	1 / х	1 / х2	у / х	ух
1	75	10	0,0133	0,0001778	0,1333	10,2
2	90	9,2	0,0111	0,0001235	0,1022	9,3
3	120	8,1	0,0083	0,0000694	0,0675	8,2
4	150	7,8	0,0067	0,0000444	0,0520	7,6
5	180	7.9	0,0056	0,0000309	0,0439	7.1
6	220	7,0	0,0045	0,0000207	0,0218	6,7
7	300	6,1	0,0033	0,0000111	0,0203	6,12
8	450	5,8	0,0022	0,0000049	0,0129	5,8
9	600	5,3	0,0017	0,0000028	0,0088	5,6
10	800	5,0	0,0013	0,0000006	0,0062	5,4
Сумма	—	72,2	0,0580	0,0004871	0,4789	—

Подставляя в это уравнение значение х, получим теоретиче­ские уровни издержек обраще­ния (ух), приведенные в последнем столбце табл. 12.14. На графике (рис. 12.4) наглядно видно вы­равнивание эмпирической ломанной линии связи по гиперболе.

Выравнивание по полулогарифмической кривой. (самостоятельно - реферат)

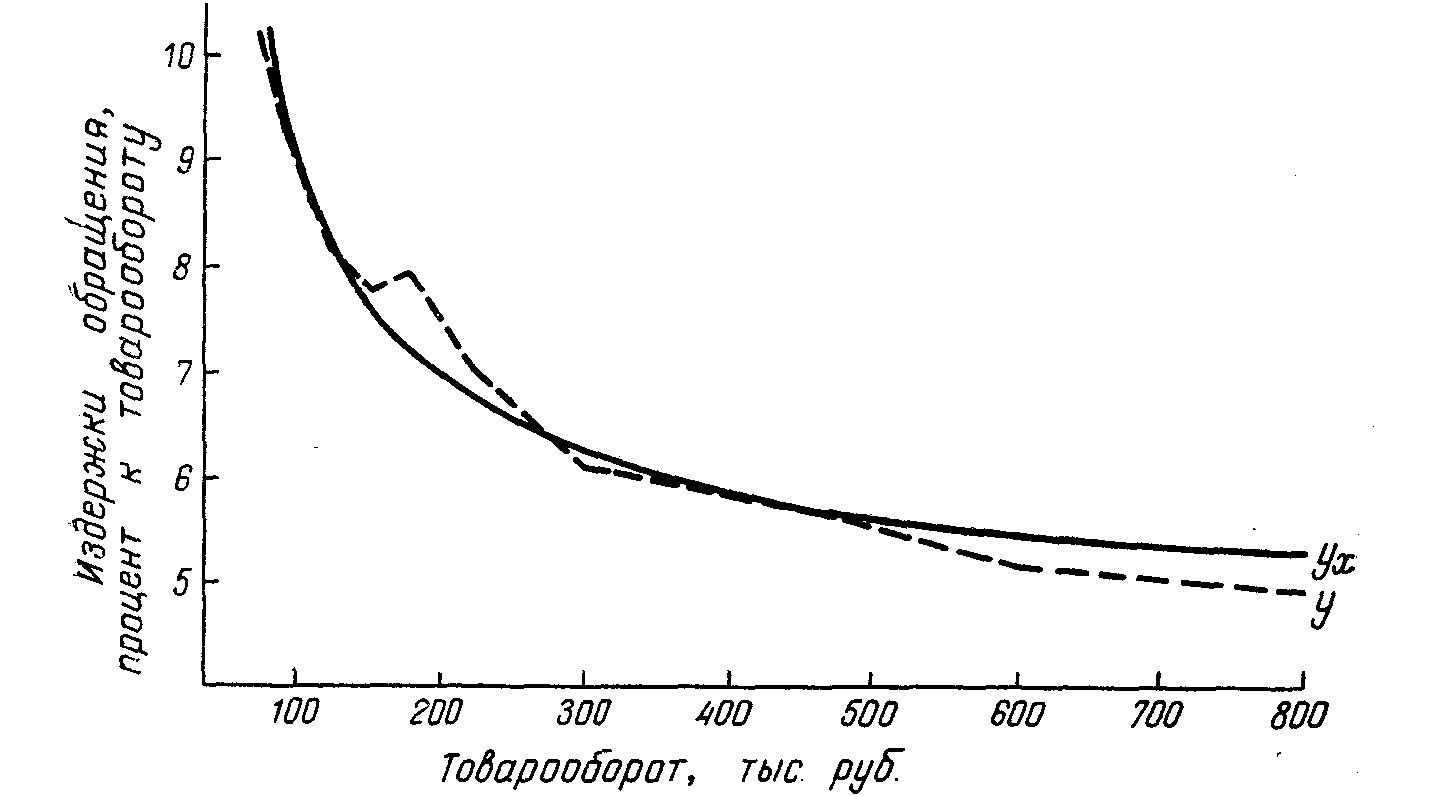
Рис. 12.4. График корреляционной зависимости между размером товаро­оборота магазина (х) и уровнем издержек обращения (у)

Выравнивание по параболе второго порядка. В качестве примера здесь приведем зави­симость урожая у от величины осадков х¹. С увеличением осадков урожайность возрастает, но до из­вестного предела, а затем начинает падать. Такую зависимость хорошо отображает пара­бола второго порядка:

Решение этих уравнений можно упростить, если ввести в них вместо значений х отклонения х от средней (х—х-). Тогда урав­нения примут вид:

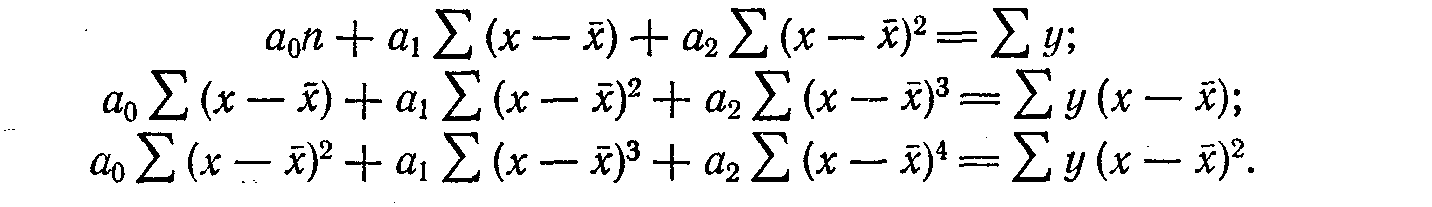
Таблица 12.15 Выравнивание по параболе второго порядка

Осадки, см (х)	Урожай, ц с 1 га (у)	х - х -	(х - х -)2	у (х - х -)	у(х - х -)2	(х - х -)4	ух
10	4,2	-40	1600	—16,8	6720	2 560 000	5,1
20	12,6	—30	900	—378	11340	810000	10,6
30	14,8	-20	400	—296	5920	160000	15,0
40	16,8	—10	100	—168	1680	10000	18,4
50	21,0	0	0	0	0	0	20,8
60	22,2	10	1 100	222	2220	10000	22,1
70	22,8	20	400	456	9120	160 000	22,3
80	21,8	30	900	654	19620	810000	21,6
90	19,4	40	1 600	776	31 040	2 560 000	19,8
450	155,6	—	6000	1098	87660	7 080 000	155,7

Х- = 450 / 9 = 50.

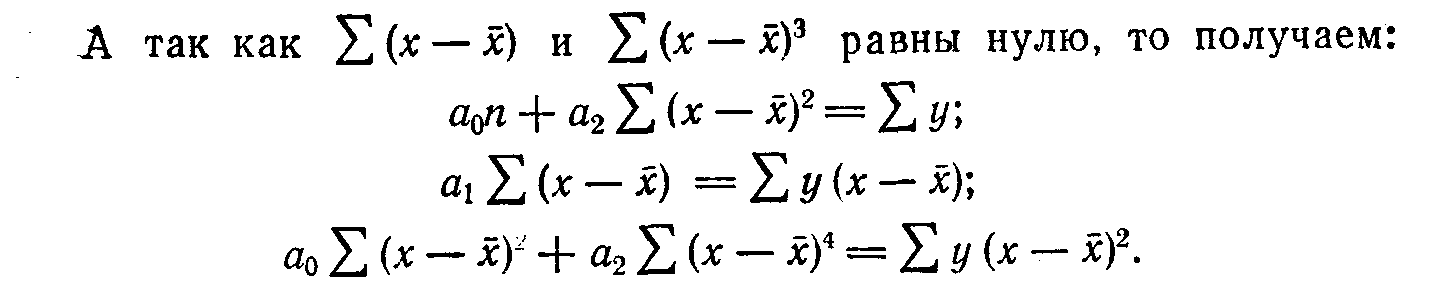
В первых двух столбцах табл. 12.15 приведены исходные дан­ные об урожае и количестве выпавших осадков, в последующих

пяти столбцах — данные, необходимые для расчета параметров параболы. Подставим эти данные в уравнения:

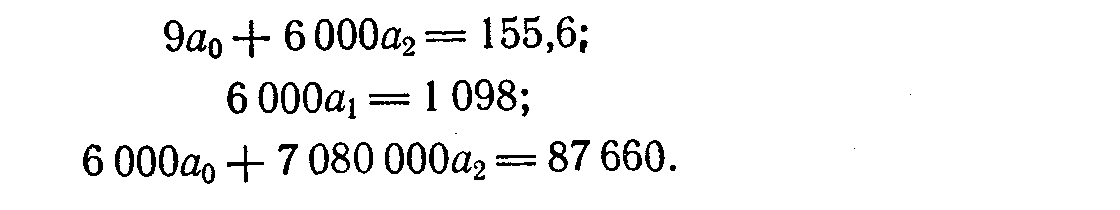
Из второго равенства определяем, что 01 = 0,183, а из первого и третьего уравнения опреде­ляем величины параметров а_о == 20,768 и а₂ = -0,005.

Следовательно, теоретическое уравнение связи принимает та­кой вид:

у_х = 20,768 + 0,183(х - х-) - 0,005 (х - х-)²

В последней колонке табл. 12.15 приведены у_х, рассчитаны по этому уравнению. Они нане­сены и на график, показывающий выравнивание эмпирических данных по параболе второго по­рядка (рис. 12.6).