80

Лекция 6 выборочное наблюдение, (начало "ряды динамики")

1. Теоретические основы выборочного наблюдения

Понятие о выборочном наблюдении и его задачах. Выборочным называется такое наблю­дение, при котором характеристика всей совокупности единиц дается по некоторой их части, отобранной в случайном порядке. Выборочное наблюде­ние - наиболее распро­страненный вид не­сплошного наблюдения в советской ста­тистике.

Широкое распространение выборочных наблюдений объясняется тем, что они требуют зна­чительно меньше сил и средств, чем сплош­ные, позволяют быстрее подводить итоги и более тщательно орга­низовать и провести наблюдение, а следо­вательно, дают и более точные резуль­таты, чем сплошные. Выборочные наблюде­ния при­меняют также для проверки результатов сплошных наблюдений.

Кроме того, нередко выборочное наблюдение является единст­венно возмож­ным.

Генеральная и выборочная совокупность, доля и средняя.

Вся совокупность единиц называется генеральной совокупностью, и ее чис­ленность обозначается N, а та часть совокупно­сти единиц, ко­торая подвергается выборочному обследованию, называется выбо­рочной совокуп­ностью, ее числен­ность обозначается n.

При выборочном наблюдении имеют дело с двумя категориями обобщающих показателей: относительными и средними величи­нами.

сводный показатель для генеральной со­вокупности называется ге­неральной долей, или долей в генераль­ной совокупности, и обозначается латинской буквой р, а для вы­борочной совокупности - выборочной долей, или частостью, .

Кроме измерения доли перед выборочным наблюдением может стоять задача измерения среднего значения варьирующего приз­нака во всей совокупности.

Среднее значение варьирующего признака во всей совокупности называется генеральной средней (х-), а среднее значение признака у единиц, которые под­верглись выборочному наблю­дению,—вы­борочной средней (х- - -).

Понятие об ошибке выборки. Задача выборочного наблюде­ния — дать вер­ное представле­ние о сводных показателях всей со­вокупности фактов на основе не­которой части их, подвергну­той обследованию.

Поскольку речь идет о варьирующих признаках и изучают не всю совокуп­ность единиц, а только часть их, то можно заранее ска­зать, что сводные показа­тели по этим признакам у части единиц совокупности почти никогда не будут аб­солютно совпадать со сводными показателями всех единиц совокупности.

Возможные пределы отклонений выборочной доли и выбороч­ной средней от доли и средней в генеральной совокупности носят название ошибки выборки (иначе она называется ошибкой ре­презентативности).

Надо различать ошибки выборки и ошибки регистрации.

По своей природе ошибки выборки могут быть тенденциоз­ными и случай­ными, (исключая, ситуации когда будут отобраны лучшие или худшие еди­ницы для выборочного обследования). Отбор конкретных единиц должен быть произве­ден не по усмотре­нию того лица, которое проводит обследование, а в случайном порядке.

Если принцип случайного отбора не соблюдается, то при­менить теоремы за­кона больших чи­сел нельзя, так как эти тео­ремы выведены для закономерностей, возникающих в случайном про­цессе.

Формулы средней ошибки выборки. При соблюдении принципа случайного отбора ошибка выборки определяется прежде всего численностью выборки. Чем больше численность выборки при про­чих равных условиях, тем меньше величина ошибки выборки.

Ошибка выборки также определяется степенью варьирования изучаемого при­знака, а степень варьирования характеризуется в статистике средним квадратом отклонений - дисперсией: ² или р(1—р) (для альтернативного признака).

У всех единиц сово­купности одинаковое значение признака, то величина дис­персии будет равна 0. Не будет и ошибки выборки, так как любая единица ге­не­ральной совокупности будет совершенно точно ха­рактеризовать всю совокупность по этому признаку.

Зависимость величины ошибки выборки от ее абсолютной чис­ленности и от степени варьи­рования признака находит выражение в формулах средней ошибки выборки. Она обозначается греческой буквой  (мю). Есть две формулы средней ошибки выборки.

Когда выборочно измеряется среднее значение признака, фор­мула средней ошибки выборки имеет такой вид:

где ( - средняя ошибка выборки;

² - дисперсия варьирующего признака;

п - численность единиц выборочной совокупности.

Для измерения средней ошибки доли альтернативного признака применяют другую фор­мулу, которая имеет вид

где р - доля признака в генеральной совокупности (например, если процент брака в продук­ции составляет от всей продукции 0,5 %, то р = 0,005); п - численность единиц выборочной сово­купности.

1. Математическое доказательство этих формул исходит из схемы так называемой повтор­ной выборки. Суть ее заключается в том, что общая численность единиц генеральной совокуп­ности в процессе выборки остается неизменной. Ту или иную единицу совокупности, попавшую в вы­борку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет рав­ную возможность со всеми прочими единицами при отборе дру­гих единиц вновь попасть в вы­борку. Такая схема выборки на­зывается схемой повторной выборки.

при бесповторной выборке чис­ленность единиц генеральной совокупности сокра­щается в процессе выборки. Применительно к бесповторной выборке в приведенные ранее формулы средней ошибки выборки необходимо до­бавить дополнительный множитель в подкоренное вы­ражение:

Следовательно, для бесповторной выборки формулы средней ошибки выборки примут та­кой вид:

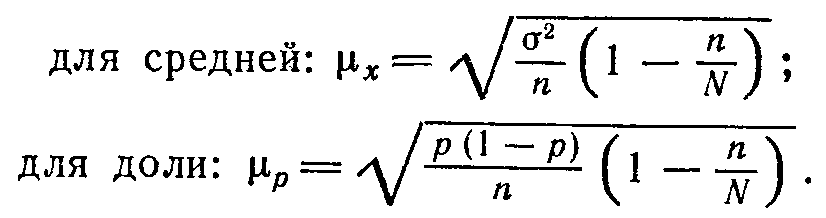
Пред­положим, что производится 225 наблюдений в первом случае из генеральной совокуп­ности в 4500 единиц и во втором — из гене­ральной совокупности в 225000 единиц. Пусть дис­персии в обоих случаях равны 25. Тогда в первом случае при 5 %-ном отборе ошибка выборки составит:

Во втором случае при 0,1 %-ном отборе ( 225 / 225000) она будет равна:

с определенной степенью веро­ятности мы можем утверждать, что отклонения выборочных ха­рактеристик от генеральных не превысят некоторой величины, ко­торая называется предель­ной ошибкой выборки. Предельная ошибка выборки (она обозначается греческой буквой «дельта» — Д) связана со средней ошибкой следующим равенством:

Приводим краткую выдержку из таблицы значений интеграла вероятностей (табл. 9.1 - в таб­лице выделены t =1,96 с вероят­ностью 0,95, t = 2,58 с вероятностью 0.99 и t = 3,28 с вероятно­стью 0,999, которым на практике часто пользуются).

Таблица 9.1

Значение вероятности при разной величине коэффициента доверия (t)

t	Вероятность	t	Вероятность	t	Вероятность
1,0	0,6827	1,8	0,9281	2,5	0,9876
1,1	0,7287	1,9	0,9426	2,58	0,99
1,2	0,7699	1,96	0,95	2,6	0,9907
1,3	0,8064	2,0	0,9545	2,7	0,9931
1.4	0,8385	2,1	0,9643	2,8	0,9949
1.5	0,8664	2,2	0,9722	2,9	0,9963
1,6	0,8904	2,3	0,9786	3,0	0,9973
1,7	0,9109	2,4	0,9836	3.28	0,9990

Расчет необходимой численности выборки. Приведенные форму­лы для оп­ределения вели­чины ошибки выборки дают возможность не только определять эти ошибки, но и рассчитывать предваритель­но, какую необходимо взять числен­ность выборки, чтобы ошибка выборки не пре­вышала определенных заданных размеров. В прак­тике при проектировании выборочного наблю­дения всегда опре­де­ляют его численность.

Под точностью понимается допустимая ошибка выборки.

Если в формулу ввести коэффициент доверия, то она примет такой вид:

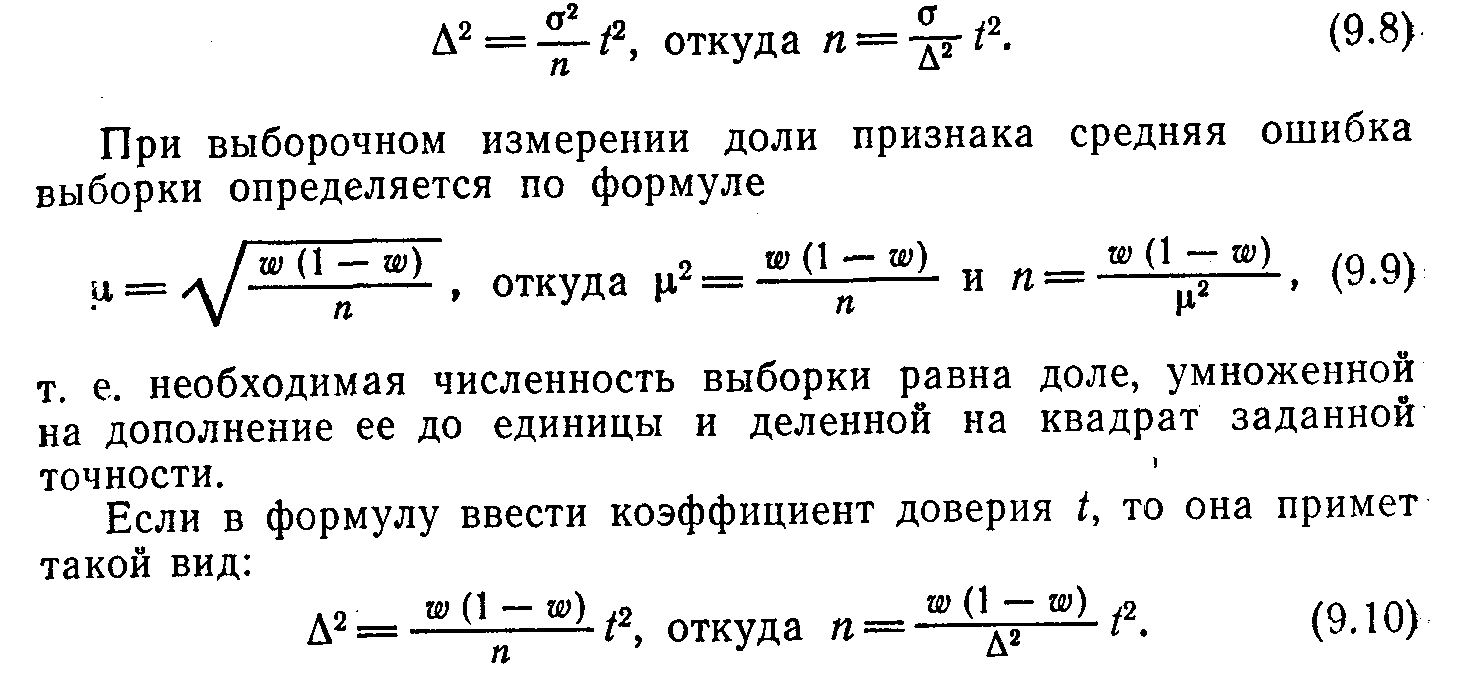
2. Способы формирования выборочных совокупностей. Нерайонированный и районированный отбор.

Таким отбором является собст­венно-случайным рай­онированным отбором бу­дет такой, когда единицы отбираются из отдельных частей (групп), на которые предварительно разбивается генеральная совокупность с полным их охватом. Примером районированного отбора является отбор предприятий по отраслям, сту­дентов института — по отдельным курсам и факультетам.

Собственно-случайный отбор. Собственно-случайный отбор дает лотерея или жеребьевка.

Механический отбор. Однако на практике собственно-случай­ный отбор при­менить бывает сложно, и поэтому его используют очень редко. Обычно приме­няют механический отбор единиц вы­борочной совокупности, который организо­вать значительно легче. При механическом отборе 100 студентов из 1000 посту­пают так составляют алфавитный список, в который включают всех сту­дентов, и определяют интервал, равный частному от деления чис­ленности генеральной сово­купности на численность выборочной совокупности. В нашем примере интер­вал равен 10 (1000 : 100). Значит, по составленному в алфавитном порядке списку будем механически выбирать каж­дого десятого студента. Интервал при механиче­ском отборе равен обратной величине от­носительного объема выборки: например, при 5 % -ной выборке интервал равен 20 (1:0,05), при 2 %-ной—50 (1:0,02) и т. д.

Типический отбор с механической выборкой. Часто имеют дело с неодно­родными по изу­чаемым показателям совокупностями. В этом случае обычно при­бегают к предварительному районирова­нию генеральной совокупности, т. е. раз­бивают на группы (на от­дельные типы) по признакам, от которых зависят изучае­мые по­казатели. Внутри этих групп производится механи­ческий отбор единиц выборочной совокупности. Такой способ отбора называет­ся типическим отбором с механической выборкой или механиче­ским отбором с предварительным райони­рова­нием. Типический отбор выгодно применять при большой дисперсии группо­вых средних, когда велика межгрупповая вариация.

Многоступенчатая выборка. Типический отбор часто сочетают с несколь­кими стадиями (ступенями) отбора. При этом каждая стадия имеет свою единицу отбора. Такая выборка называ­ется многоступенчатой.

Многофазная выборка. Многофазная выборка отличается от многоступенча­той тем, что на всех ступенях выборки сохраняется одна и та же единица отбора.

Комбинирование выборочного наблюдения со сплошным. Соче­тание вы­борочного об­следования со сплошным характерно для многофазовой выборки, хотя она может быть организо­вана и без такого комбинирования. Комбинирование выборочного наблю­дения со сплошным ин­тересно тем, что оно позволяет лучше про­верить типичность выборочных данных, сопоставляя основные показатели по выборочным и массовым данным.

Серийная выборка. Для всех рассмотренных видов случайного отбора необ­ходим отбор от­дельных единиц выборочной совокуп­ности, однако применяют и такие способы отбора, при ко­торых в выборку попадают не отдельные единицы, а целые серии (гнезда). Такой способ отбора называется серийным. Например, при 10 %-ном выборочном обследовании качества продукции мож­но брать каждую десятую выпущенную единицу продукции, а можно организовать выборку так, что через каждые 9 часов в течение одного (десятого) часа вся выработанная в те­чение этого часа продукция будет подвергнута сплошному обследованию.

Моментные наблюдения. Особым видом выборочного наблюде­ния является моментное на­блюдение, получившее в последнее время широкое распространение в промышленности и других от­раслях народного хозяйства. Суть его состоит в том, что на опре­деленные моменты времени фиксируется наличие отдельных эле­ментов изучаемого процесса.

Малая выборка. Под малой выборкой понимается такое выбо­рочное наблю­дение, числен­ность единиц которого не превышает 20.

(Самостоятельно).