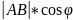Обозначения

Обозначение векторов базиса может быть в принципе произвольным. Часто используют какую-нибудь букву с индексом (числовым или совпадающим с названием координатной оси), например:

или

— типичные обозначения базиса двумерного пространства (плоскости).

или

— трехмерного пространства. Для трехмерного пространства часто по традиции используется и обозначение

Представление какого-то конкретного (любого) вектора  пространства в виде линейной комбинации векторов базиса (суммы базисных векторов числовыми коэффициентами), например

или

или, употребляя знак суммы  :

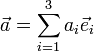
называется разложением этого вектора по этому базису.

Числовые коэффициенты   называются коэффициентами разложения, а их набор в целом — представлением (или представителем) вектора   в базисе  (Разложение вектора по конкретному базису единственно; разложение одного и того же вектора по разным базисам — разное, то есть получается разный набор конкретных чисел, однако в результате при суммировании — как показано выше — дают один и тот же вектор).

Координаты вектора.

Декартовой системой координат в пространстве называется совокупность точки и базиса.

Точка носит название начала координат. Прямые проходящие через начало координат в направление базисных векторов, называются осями координат; первая- ось абсцисс, вторая – осью ординат, третья- осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями. Компоненты x,y,z, называются координатами точки.

Чтобы найти координаты вектора нужно из координат конца вычесть координаты начала.

Декартова прямоугольная система координат.

Опр.Базис называется ортонормированным, если его векторы попарно ортогональны и по длине равны единице.

Опр.Декартова система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат.

Координаты точек в прямоугольной системе координат, равны расстоянию точки до нужной плоскости.

Относительно \координат вектора всё также.

Проекция вектора на ось.

Проекция вектора на AB на ось L называется величина = длине вектора A’B’ взятая с +, если вектор AB соноправлен L, и с - , если AB противоположно направлен L.

Проекция AB=

Свойства проецкии:

1)Проекция суммы векторов = сумме проекций.

2)

10.Линейные комбинации 2, 3, 4-х векторов. Линейная зависимость и независимость векторов.

     Линейной комбинацией векторов   называют вектор

     

где   - коэффициенты линейной комбинации.

Если   комбинация называется тривиальной, если   - нетривиальной.

Система векторов называется линейно независимой, если их линейная комбинация равна 0, выполняется в том случае только, если все коэф. а если хотя бы один из них не равен 0,то линейно зависимая.

11.Скалярное произведение векторов. Свойства и выражение в декартовых координатах.

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Скалярное произведение векторов  ,   обозначается символом   (порядок записи сомножителей безразличен, то есть  ).

Если угол между векторами  ,   обозначить через  , то их скалярное произведение можно выразить формулой

 (1)

Скалярное произведение векторов  ,   можно выразить также формулой

, или  .

Из формулы (1) следует, что  , если   - острый угол,  , если   - тупой угол;   в том и только в том случае, когда векторы   и   перпендикулярны (в частности,  , если   или  ).

Скалярное произведение   называется скалярным квадратом вектора и обозначается символом  . Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:

.

Если векторы   и   заданы своими координатами:

,  ,

то их скалярное произведение может быть вычислено по формуле

.

Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов

.

Угол   между векторами

,  ,

дается формулой  , или в координатах

.

Проекция произвольного вектора   на какую-нибудь ось u определяется формулой

,

где   - единичный вектор, направленный по оси u. Если даны углы  ,  ,  , которые оси u составляет с координатными осями, то   и для вычисления вектора   может служить формула

.

Свойства:

• условие ортогональности^[2] (перпендикулярности) векторов   и  :

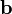2. a*b=b*a

3.(£*a)*b=£*(a*b)

4.(a+b)*c=a*c+b*c

5.

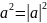
Применение:

1)Работа силы F по перемещению материальной точки . А(работа)=F*AB(вектор).

2.Вычисление косинуса угла между векторами.