2.21. Преобразования Лапласа распределений нсв.
Пусть A(t) – закон распределения непрерывной неотрицательной случайной величины. Соответствующая плотность a(t), t≥0.
Тогда, преобразование Лапласа для плотности распределения:
â
(s)
=
Преобразование Лапласа для закона
распределения: Â(s)
=
Поскольку A(t)
=
,
то для преобразований справедливо:
Â(s)
=
С
лучайные
величины x
и y
называются взаимно независимыми, когда
условие, что одна из величин приняла
конкретное значение, никак не влияет
на распределение второй величины. Если
а и b
2 независимые положительные случайные
величины, а r
= a
+ b,
то
Преобразование
Лапласа можно определить, пользуясь
теоремой для преобразования Лапласа:
Начальный момент
k
вероятностного распределения определяется:
При известном
:
Пределы позволяют оценить:
Математическое ожидание:
Второй момент:
Дисперсию:
Среднее квадратическое отклонение:
Коэффициент вариации:
2.22. Производящие функции распределений дсв.
Рассмотрим дискретную
случайную величину r,
которая распределена равномерно на
интервале [a,
b],
b≥a.
Производящая функция вероятностей
определяется формулой:
Свойства
производящей функции распределения
дсв:
1
.
Из определения производящей функции
вероятностей дсв следует:
2. Пусть k≥0
– кратность полюса производящей функции
в т. z=0.
Тогда
3. Пусть z=0
– нуль порядка k≥0
производящей функции. Тогда
4. Если рассматривается
сумма 2х неотрицательных независимых
дсв r
= a
+ b,
то вероятности задаются сверткой:
Вычисление моментов распределения с использованием производящих функций:
Первый момент:
Второй момент:
Дисперсия:
Среднее квадратическое отклонение:
2.23. Использование преобразования Лапласа для представления распределений дсв.
Плотности распределения можно использовать для определения детерминированных случайных величин (величин, принимающих некоторое значение в вероятностью 1). Для записи функции плотности можно использовать дельта функцию.
Свойства дельта функции:
1.
2.
просеивающее свойство:
Пусть задана детерминированная случайная величина а.
Вероятность a≥A
= 1(t-A).
Вычислим преобразование Лапласа:
(из
просеивающих свойств дельта функции).
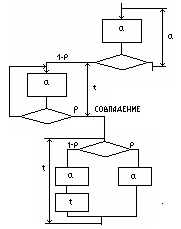
3.24. Композиция, вероятностные переходы и циклы с вероятностным повторением участка программы.
Композиция функций. ВЕРОЯТНОСТНЫЕ ПЕРЕХОДЫ. Связывая с условным переходом понятие вероятности, можно прийти к нескольким схемам. К числу довольно простых относятся марковские модели программ. Эти модели не содержат вершин, определяющих циклические переходы. Они основаны на представлении модели программы в виде ориентированного графа ГV,L, где V представляет собой множество вершин с определенными параметрами, а L множество дуг, отражающих возможные переходы от вершины i к вершине j.
3.25. Задача о поиске элемента в массиве.
Дан массив, содержащий данные, которые заранее не упорядочены. Мы последовательно просматриваем элемент за элементом, и когда нужное значение найдено, печатаем его индекс.
