4.36. Дцм с произвольным временем пребывания в состояниях с одним поглощающим состоянием.

Марковские цепи с произвольным временем пребывания процесса в состояниях

В общем случае нас будет интересовать время, проводимое процессом в состоянии j. Будем считать это время случайной величиной, независимой от др. случайных величин, определенных в этом процессе. Обозначим время, проводимое процессом в состоянии j – a_j⁽ⁿ⁾, (n) говорит о том, что это время, проведенное процессом в состоянии j после n-ного попадания в это состояние. a_j⁽ⁿ⁾(t) – плотность распределения этой случайной величины. Сделаем предположение, что эта плотность не зависит от n. Пусть после некоторого шага (n) процесс находится в состоянии k. Тогда дальнейшее его развитие происходит по след. схеме: k → задержка на a_k → переход к следующему состоянию. Определяется время, через которое процесс попадет в это следующее состояние так: . Очевидно, что Тn тоже является с/в, a_k не зависит от Тn. Отсюда - это преобразование Лапласа плотности распределения того времени, которое процесс проведет за n+1 шаг при условии, что на n-м шаге он находится в состоянии k.

Процессы с одним поглощающим состоянием

Заданы: π – матрица переходов, - ПЛ плотности распределения времени пребывания процесса в соответствующем состоянии. Обозначим: - ПЛ времени продвижения процесса из состояния i в поглощающее состояние.

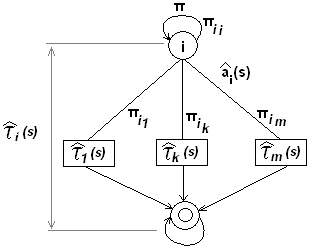
0- поглощающее состояние.

1.7 Условная вероятность

Введем понятие независимых и зависимых событий. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет. Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р(А|В) или P_B(A).Условная вероятность события А при условии наступления события В равна Р(А|В)= Р(АB) /P(B) ,Эта формула называется формулой условной вероятности. Условие независимости события А от события В можно записать в виде: Р(А|В)= Р(А),а условие зависимости: Р(А|В)  Р(А).

1.7 – 1.10 Условная вероятность. Вероятность произведения событий. Независимость событий. Формула полной вероятности.

Пусть из коробки(бесконечная емкость) вынимаются карандаши:

А-красный Т-твердый

Б-черный М-мягкий

С-белый

Карандаши могут быть или твердыми или мягкими. Рассмотрим серию из n испытаний:

А	B	А	А	А	С	B	А	B	B	С
Т	М	М	Т	Т	Т	Т	М	Т	М	Т

Относительные частоты событий:

Pn(T/A)=mT(A)/mA=3/5

Pn(M/A)=mM(A)/mA=2/5

Pn(T/B)=mT(B)/mB=2/4=1/2

Pn(M/B)=mM(B)/mB=2/4=1/2

Pn(T/C)=mT(C)/mC=2/2=1

Pn(M/C)=mM(C)/mC=0

Это означает, что нас интересует событие Т, только в случае события А.

Пусть мы вынули карандаш из коробки, нас интересует событие, состоящее в том, что вынутый красный карандаш является твердым. Нас будет интересовать вероятность этого события. А*Т-такое событие определяется как произведение событий. Частота появления этого события есть Pn(A*T)=3/11=mAT/n=mAT/n*mA/mA=Pn(T/A)*Pn(A)- формула произведения вероятностей. При n стремящимся к бесконечности получим:

P(A*T)=P(T/A)*P(A)

В том случае, если P(T/A)=P(T/B)=P(T/C) то, говорят о том, что событие «цвет карандаша» и «твердость» независимые друг от друга. Вводим обозначение P(T).

P(A*T)=P(A)*P(T). Пользуясь относительными частотами и вычисляя пределы можно показать, что

P(T)=P(T/A)*P(A)+P(T/B)*P(B)+P(T/C)*P(C) - формула полной вероятности.