19.Аналитические методы выявления неслучайной составляющей временного ряда. Модели кривых роста.

Вслучае аналитического сглаживания фактические уровни ряда заменяются теоретическими, рассчитанными по определенной кривой, отражающей общую тенденцию изменения показателя во времени. Эти кривые получили название кривых роста.

Аналитическими методами выявления неслучайной составляющей с помошью кривых роста реализуют в рамках модели регрессии где в роле зависимой переменной уt а в роле объясняющей переменной время t.

Аналитическое вравнивание состоит из 2 этапов:

1)выбор вида кривой

2)определение численных параметров кривой

Кривые роста 3 типа:

1)без предела роста

2)с пределом роста без точки перегиба

3)с пределом роста и точкой перегиба

Первая группа полиномиальные кривые: параметр   называют линейным приростом, параметр  – ускорением роста, параметр  – изменением yскорения роста.

Для полинома первой степени характерен постоянный закон роста. Если рассчитать первые приросты по формуле   то они будут постоянной величиной, равной  . Если первые приросты рассчитать для полинома второй степени, то они будут иметь линейную зависимость от времени и ряд из первых приростов U_t— на графике будет представлен прямой линией. Вторые приросты   для полинома второй степени будут постоянны.Для полинома третьей степени первые приросты будут полиномами второй степени, вторые приросты будут линейной функцией времени, а третьи приросты, рассчитываемые по формуле , будут постоянной величиной. Полиномиальные кривые роста можно использовать для аппроксимации (приближения) и прогнозирования экономических процессов, в которых последующее развитие не зависит от достигнутого уровня.

Показатель	Характер изменения показателя во времени	^ Тип кривой роста;	Уравнение
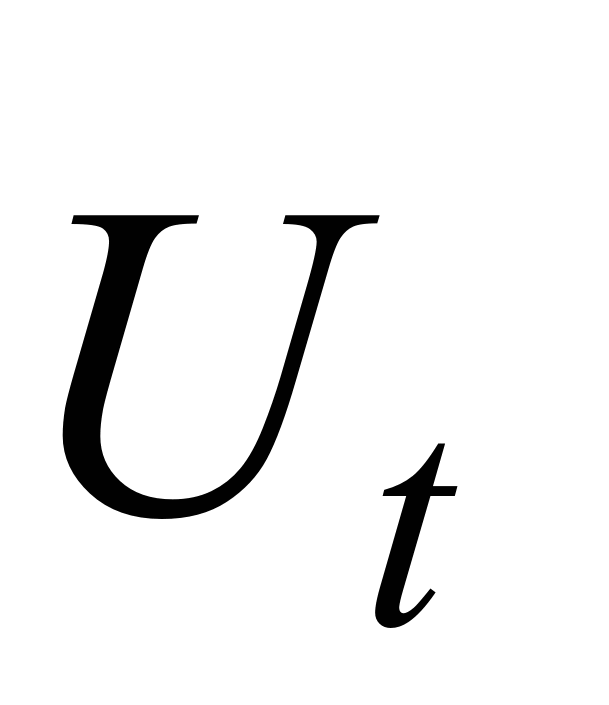
Первый средний прирост	Примерно одинаковы	Полином первого порядка (прямая)
Первый средний прирост	Изменяются линейно	Полином второго порядка (парабола)
Второй средний прирост	Изменяются линейно	Полином третьего порядка (кубическая парабола)
	Примерно одинаковы	Простая экспонента	,
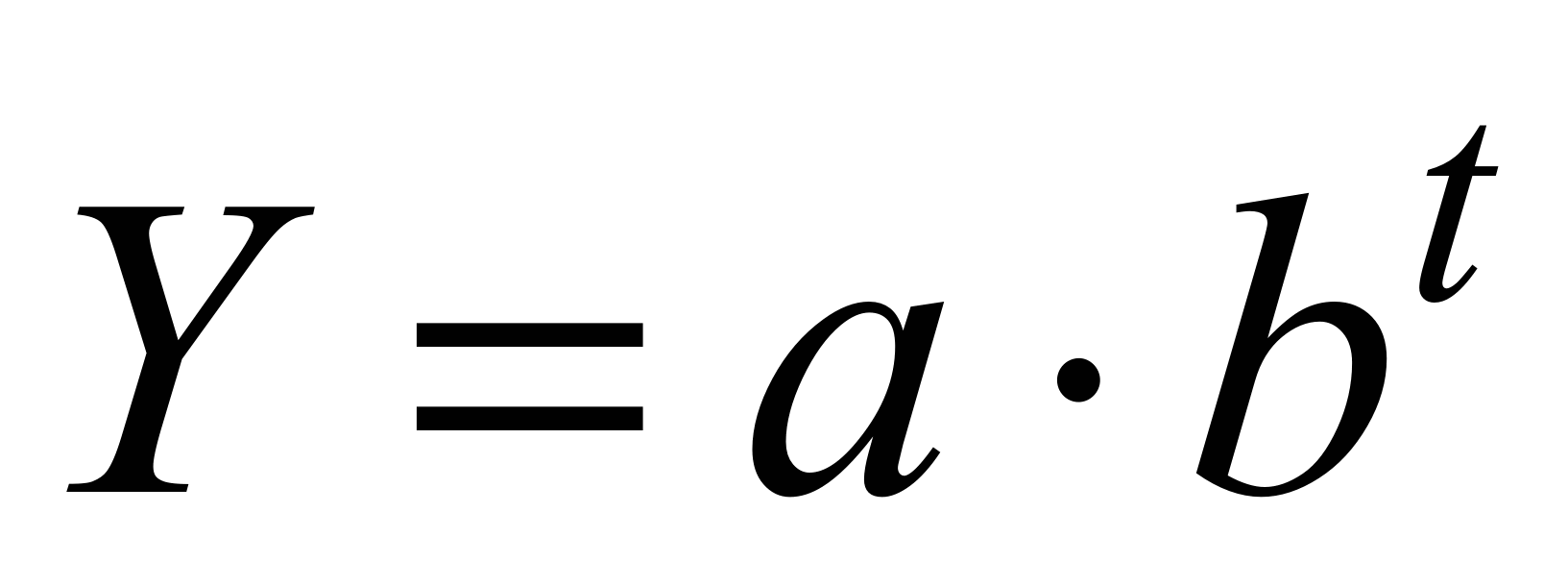	Изменяются линейно	Модифицированная экспонента
	Изменяются линейно	Кривая Гомперца
	Изменяются линейно	Логистическая кривая

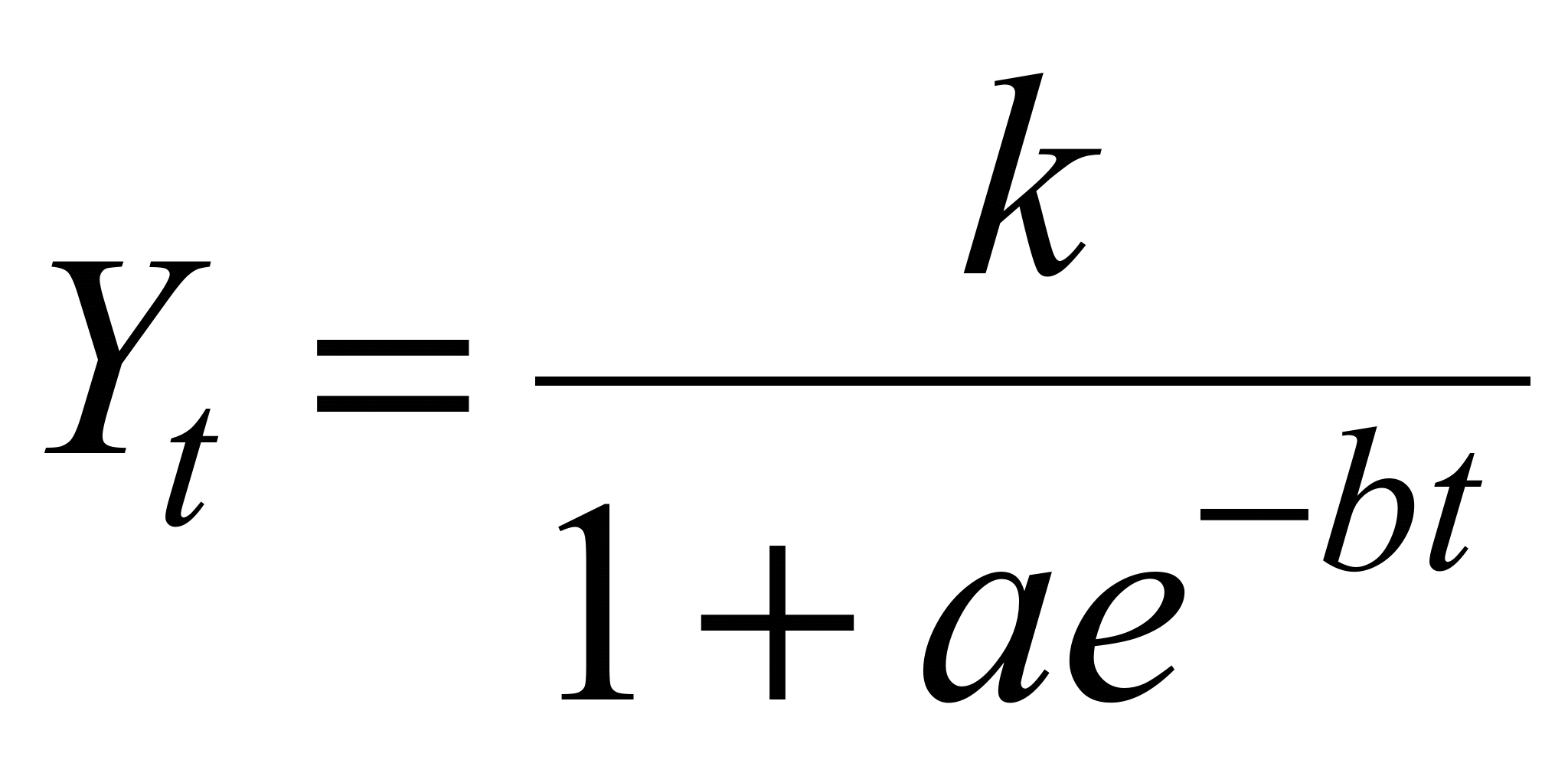
24. Методы механического сглаживания временных рядов. Метод простой скользящей средней.

Суть методов механического сглаживания заключается в следующем. Берется несколько первых уровней временного ряда, образующих интервал сглаживания. Для них подбирается полином, степень которого должна быть меньше числа уровней, входящих в интервал сглаживания; с помощью полинома определяются новые, выровненные значения уровней в середине интервала сглаживания. Далее интервал сглаживания сдвигается на один уровень ряда вправо, вычисляется следующее сглаженное значение и т. д.

Метод простой скользящей средней.Самый простой метод сглаживания скользящее среднее, в котором каждый член ряда заменяетс япростым или взвешенным средним m соседних

членов, где m - ширина интервала сглаживания. Вместо среднего можно использовать медиану значений, попавших в интервал сглаживания. Если необходимо сгладить мелкие беспорядочные колебания, то интервал сглаживания берут по возможности большим. Если нужно сохранить более мелкие колебания, интервал сглаживания уменьшают. При прочих равных условиях интервал сглаживания рекомендуется брать нечетным. Для вычисления сглаженных уровней рядаYt применяется формула: вычисления сглаженных уровней рядаYt

применяется формулой:

,где p=m-1/2(при нечетном m)

В результате такой процедуры получаются(n-m+1)сглаженных значений уровней ряда; при этом первые р ипоследние р уровней ряда теряются (не сглаживаются). При четных значениях т, после процедуры сглаживания обычно поводят центрирование полученно горяда (находят средние значения двух последовательных скользящих средних).Данный метод применим лишь для рядов, имеющих линейную тенденцию. Если для процесса характерн онелинейное развитие, то простая скользящая средняя может привести к существенным искажениям.

29. Оценка точности и качества моделей, выбор наилучшей модели Оценка качества модели оценивается стандарным для математических моделей образом:по адкватности и точности на основе анализа остатков регрессии.

Проверка случайностив ряду остатков (критерий поворотных точек, Критерий серий, критерий восходящихи нисходящих серийи пр.)

Критерий поворотных точек(пиков)

Каждый элемент ряда ei сравнивается сдвумя рядом стоящими элементами ei−1и ei+1.

Если ei больше (или меньше) как ei−1, таки ei+1, то она считается поворотной.

Проверка равенства математического ожидания случайной компоненты нулю ( M(εi)=0 i=1,n)

Из применения МНКвытекает: =0 т.е(1)

В то же время из условия (1) необязательно должно следоватьусловие Равенства нулю математического ожидания величин εi,i=1,n). Поэтому необходима проверка выполнимости этого условия Формулируется нулевая гипотеза : H0:e=0 . Строится t статистика:

,где

На уровне значимости α гипотеза отклоняется, если расч>крит...

Проверка независимости (отсутствия автокорреляции) вряду остатков.

Корреляционная зависимость между рядом наблюдений и тем же рядом,сдвинутым на несколько шагов по времени, называется автокорреляцией.

КритерийДарбина-Уотсона (d-критерий).

Это наиболее распространенный и простой критерий (тест), выявляющий определяющий только автокорреляцию первого порядка, т.е. между рядами, сдвинутыми на однозначение (лаг=1). Оноснован на простой идее: если имеется корреляция ошибок εi, то она присутствует и в остатках ei, получающихся после применения МНК

Рассчитывается статистика d: d= (2)

Несложные вычисления позволяют проверить, что ) d≈2(1−ρ),где ρ- выборочный парный коэффициент корреляции между соседними уровнями ряда. Если автокорреляция отсутствует, то ρ=0, следовательно, 2≈d. В случае функциональной зависимости ρ=1, а d≈0. Таким образом, интервал изменения d: 0≤d≤4. Близость статистик d к 4 свидетельствует об отрицательной автокорреляциио статков. Такая закономерность поведения последовательных может встретиться при работе, на пример с полугодовыми данными показателей с сезонным характером изменений. Близость d к нулю означает наличие положительной автокорреляции4.

Имеются таблицы критических точе краспределения Дарбина – Уотсона По ней для заданного уровня статистической значимости α, числа наблюдений n и количества факторных переменных определяются двазначения: d1–нижняя граница и d2- верхняя граница. Расчетная величина d

сравнивается с двумя этими значениями. Возможны следующие случаи:

•0≤d<d1– существует положительная автокорреляция;

•d1≤d<d2 – область не определенностии необходимы дополнительные проверки на независимость ряда остатков;

• d2≤d≤2– автокорреляция отсутствует;

Еслиd>2, то вводим величинуd*=4−d И осуществляем для нее такую же проверку как для d. При этом, если 0≤d*<d1, то существует отрицательная автокорреляция.

Проверка ряда остатков на нормальность распределения.

Для проверки статистической значимости параметров и прогнозирования по трендовой модели, ряд остатков должен подчиняться нормальному закону распределения

RS–критерий.

По выборке рассчитывается статистика RS: здесь

Имеются теоретические таблицы критических значений величины RS.,рассчитанные для различных доверительных вероятностей в зависимости от числа переменных n .Если расчетное значение RS попадает между табулированными значениями a и b т. е. a<RS<b при выбранном уровне доверия, то принимается гипотеза о соответствии ряда остатков нормальному

закону распределения, в противном случае эта гипотеза отвергается.

Точностьмодели

Точность модели определяется на основе средней относительной ошибки

Аппроксимации

Если средняя относительная ошибка аппроксимации менее 10%, точность модели признается хорошей.