8. Выражение скалярного произведения векторов через координаты сомножителей.

Пусть

A( , B( )

9. Вычисление модуля вектора, угла между векторами, работы силы; направляющие косинусы вектора.

Основные приложения скалярного произведения

1) Вычисление работы (A), силы (F), затраченной на перемещение из точки B точку C

2) Вычисление угла между векторами

3) Вычисление проекции одного вектора на другой

10. Векторное произведение векторов, его основные свойства, геометрический и механический смысл.

Векторным произведением называется вектор , удовлетворяющий условиям:

1)

2)

3)

Свойства векторного произведения:

1) Антикоммутативность

2) Ассоциативность относительно числового множителя

3) Дистрибутивность

4) Условие коллинеарных векторов

Ненулевые векторы коллинеарны тогда и только тогда, когда их векторное произведение равно нулю

; ( )

Геометрический смысл векторного произведения:

Модуль векторного произведения численно равен площади параллелограмма, построенного на этих векторах как на сторонах.

Механический смысл векторного произведения:

Если вектор - сила, а вектор - есть радиус-вектор точки приложения силы, имеющий своё начало в точке O, то момент силы относительно точки O, - есть вектор , равный векторному произведению радиус -вектора (точки приложения силы) на силу , то есть:

11. Выражение векторного произведения векторов через координаты сомножителей.

Векторное произведение через координаты со множителем:

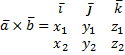
Основные приложения векторных произведений:

1) Вычисление площади параллелограмма и треугольника

2) Нахождение вектора, перпендикулярного двум данным векторам

3) Вычисление момента силы F, приложенной к точке A, относительно точки O

12. Смешанное произведение трёх векторов, его выражение через координаты сомножителей, свойства и приложения.

Смешанное произведение векторов - скалярное произведение одного из векторов на векторное произведение двух других

Выражение через координаты сомножителей

Таким образом, смешанное произведение трех векторов равно определителю, составленному из координат этих векторов.

Свойства смешанного произведения:

1) Векторно можно перемещать любую пару со множителем

2) При перестановке двух векторов, его знак меняется на противоположный

3) При круговой перестановке сомножителей, смешанное произведение не меняется

4) Ассоциативность относительно числового множителя

5) Дистрибутивность

13. Геометрический смысл смешанного произведения.

Геометрический смысл - смешанное произведение с точностью до знака равно объему параллелепипеда, построенного на этих векторах. При этом произведение имеет знак "+", если тройка правая, и знак "-", если тройка левая.

14. Условие компланарности трёх векторов.

Для того, чтобы три вектора были компланарными, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю

- компланарные

15. Уравнение линии на плоскости, прямая как линия первого порядка (необходимое и достаточное условие)

Пусть на плоскости задана некоторая линия (кривая)

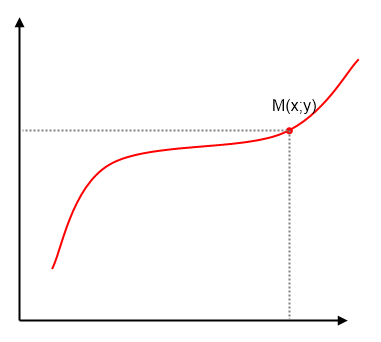
Уравнение вида F(x;y)=0 называется уравнением линии первого порядка, если его удовлетворяют каждые координаты точек, лежащих на этой кривой, и не удовлетворяют координаты точек, не лежащих на этой кривой

16. Общее уравнение прямой и его исследование.

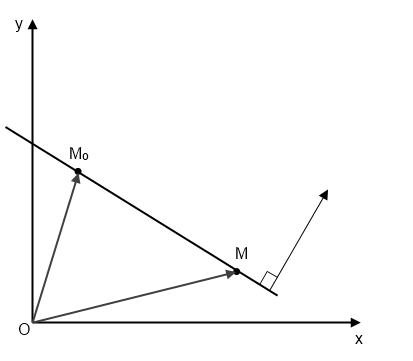
- начальная точка

- начальный радиус-вектор

- произвольная точка,

- текущий радиус-вектор

Любой ненулевой вектор, перпендикулярный прямой, называется нормальным вектором этой прямой. - нормальный вектор прямой

Уравнение прямой в векторной форме:

Через координаты со множителями:

Общее уравнение прямой:

17. Некоторые частные виды уравнения прямой: уравнение прямой с угловым коэффициентом, уравнение прямой в отрезках, уравнение прямой, проходящей через данную точку в данном направлении, уравнение прямой, проходящей через две данные точки.

С заданным угловым коэффициентом:

Уравнение прямой в отрезках: 1) С=0, (прямая проходит через т.(0;0)

2) B=0, (прямая ⏊ ox)

3)B=0, C=0, x=0 (ось ординат или || ей прямая)

4) A=0, (прямая⏊ oy)

5) A=0, C=0, y=0 (ось абсцисс или || ей прямая)

, где

Уравнение прямой, проходящей через две данные точки:

Уравнение прямой, проходящей через данную точку в данном направлении:

?