1. Определители, их основные свойства и вычисление.

М инором элемента называется определитель (n-1) порядка, полученный из исходного определителя удалением i-строки и j-столбца

Алгебраическим дополнением элемента называется минор

Следствие из теоремы Лапласа - определитель равен сумме произведений элементов какой-либо строки(столбца), умноженных на их алгебраическое дополнение.

Свойства определителя:

1. Если строки или столбцы поменять местами, то его величина не изменится

Это свойство определяет, что строки и столбцы определителя равноправны

(Операция замены строк столбцами с сохранением нумерации называется транспонированием)

2. Если все элементы строки(столбца) определителя равны нулю, то и сам определитель равен нулю.

3. Если в определителе элементы строки(столбца) имеют общий множитель, то его можно вынести за знак определителя

4. Если определитель имеет две одинаковые строки(столбца), то он равен нулю.

5. Если в определителе переставить местами две строки(столбца), то определитель изменит знак на противоположный

6. Если в определителе строки(столбцы) пропорциональны элементам другой строки(столбца), то определитель равен нулю

7. Если все элементы строки или столбца представлены в виде суммы двух слагаемых, то такой определитель можно представить в виде суммы двух определителей

8. Если к элементам некоторой строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженных на любой множитель k, то величина определителя не изменится

2. Системы линейных алгебраических уравнений, формулы Крамера.

Рассмотрим систему линейных уравнений третьего порядка:

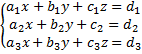
Запишем определитель системы, то есть определитель, состоящий из коэффициентов при переменных:

Пусть

Составим определители, заменяя в определителе системы столбец коэффициентов при выбранной переменной столбцом, состоящим из свободных членов:

,

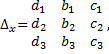
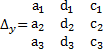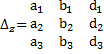
Если определитель системы отличен от нуля, то системы линейных уравнений имеют единственное решение, которое определяется формулами

,

Таким образом,

•если определитель системы отличен от нуля, то система совместная определенная (имеет 1 решение)

•если определитель равен нулю, то возможны два случая:

а) если хотя бы один определитель 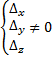, то система несовместна (решений нет)

б) если все определители 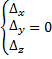, система совместная неопределенная (бесконечное множество решений)

3. Определение вектора, модуль вектора, коллинеарные и компланарные векторы, равенство векторов.

Вектором называется направленный отрезок, то есть отрезок, с указанными начальной и конечной точками

А

В

Модулем (длиной) вектора называется длина отрезка АВ -

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными

Коллинеарные векторы могут быть сонаправлены или

противоположнонаправлены

Векторы, лежащие в одной плоскости или в параллельных плоскостях, называются компланарными

Два вектора называются равными, если они компланарны, коллинеарны и их длины равны