Теория игр

В данном разделе рассматриваются элементы теории игр, связанные с анализом конфликтных ситуаций, когда есть соперничество (конкуренция) участников. Примерами таких задач является конкуренция фирм за рынки сбыта.

Другой постановкой является задача выбора партнеров для совместной деятельности, анализ и решение этой задачи относится к коалиционным играм.

Основные понятия теории игр

Пусть – участники игры.

Каждый участник имеет в своем распоряжении множество чистых стратегий (возможных ходов в этой игре):

или ;

;

.

Исход – сочетание (когда выбирает одну чистую стратегию, – другую, а – третью).

Каждый из исходов характеризуется полезностью (выигрышем) для каждого участника:

– полезность исхода для участника ;

– для участника ;

– для участника .

Решить задачу – значит найти оптимальную стратегию выбора стратегий для участников. Возможные критерии оптимальности:

– справедливость;

– устойчивость (устраивает всех участников).

Классификация игр

Если для всех участников существует конечное число чистых стратегий , , где и конечны, то такие игры являются конечными. Игры с двумя участниками и Если то эти игры называются антагонистическими (выигрыш одного влечет проигрыш другого). В этом случае достаточно задать только одну матрицу , поэтому такие игры называются матричными. В общем случае игры с двумя участниками называются биматричными.

Если для каждого участника существует только две стратегии, то такие игры называются диадическими.

Матричные игры с седловой точкой

Пусть задана для участника матрица выигрышей , которую называют платежной матрицей.

Определение 1 (доминирующая стратегия). Если для двух стратегий и выполняется условие , и существует хотя бы одна стратегия такая, что , тогда является доминирующей стратегией по отношению к , а чистая стратегия – доминируемой стратегией.

Если для пары стратегий и , и существует такая, что , тогда – доминирующая по отношению к , а – доминируемая стратегия.

Доминируемые стратегии можно исключить из матрицы , так как оптимального решения среди них не будет.

Выбираем оптимальную стратегию для участника А по принципу:

.

Величина определяет нижнюю цену игры. Выбор стратегии по этому принципу гарантирует, что выигрыш будет не меньше, чем .

Для участника B оптимальная стратегия определяется по принципу: – верхняя цена игры.

Игры, у которых , называются играми с седловой точкой.

Может быть несколько седловых точек, тогда цена игры во всех этих точках одинакова: , где – цена игры.

Пусть существуют две седловые точки . Из условий определения седловых точек следует:

.

Все эти нестрогие неравенства выполняются только в случае, когда все 4 числа равны: .

Матричные игры без седловой точки

В данном классе игр нижняя цена игры строго меньше верхней .

Смешанная стратегия – комбинация чистых стратегий с вероятностями выбора :

; .

Оптимальная смешанная стратегия: .

Для любой матрицы можно определить оптимальную смешанную стратегию: такую, что выигрыш участника , определяемый в соответствии с выражением: ,будет в интервале (для участника это проигрыш ).

Теорема о минимаксе. В матричной игре без седловой точки существует точка равновесия такая, что выигрыш участника находится в интервале , и оптимальные решения для участников находятся из условий: для – из условия ,

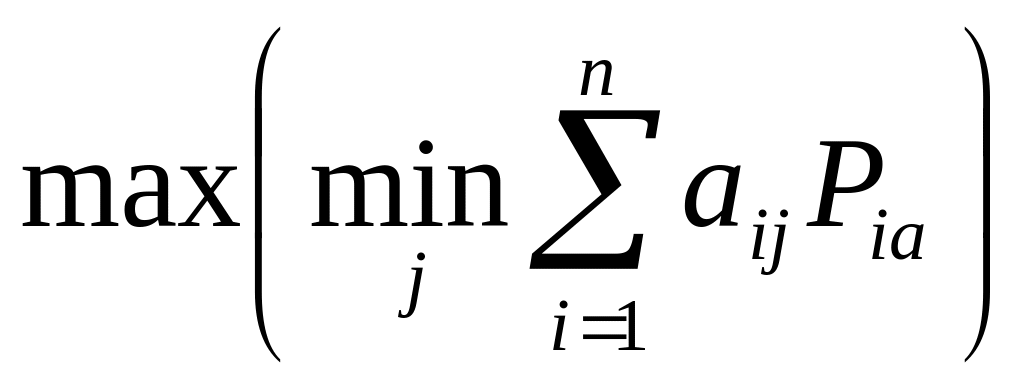для – из условия ,

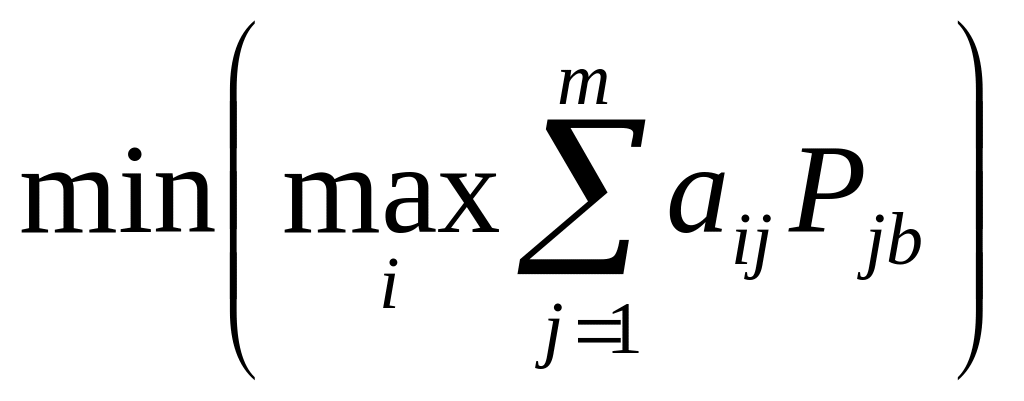– цена игры.

Определение 2 (активные стратегии). Активные стратегии для участника – это те стратегии из множества чистых , для которых .

Утверждение 1. Если участник придерживается оптимальной смешанной стратегии, то его выигрыш не зависит от стратегии участника в пределах активных стратегий участника .

Решение матричных игр 22

Каждый из участников имеет по две чистые стратегии. Матрица выигрышей для A имеет вид:

.

Элементы матрицы таковы, что , т.е. седловой точки нет.

В качестве решения игры необходимо получить смешанные стратегии .

Для определения также составим уравнение:

;

; .

Цена игры (выигрыш для участника ) будет равна:

.