2.3. Математическая постановка задачи оптимального проектирования цифровых фильтров.

Проектирование цифровых фильтров частотной селекции с точки зрения современных представлений теорий цифровых цепей включает в себя три основных этапа:

1. выбор класса цифровых цепей и аппроксимация желаемых частотных характеристик фильтра в пространстве функций, строго воспроизводимых заданным классом цифровых цепей;

2. выбор метода проектирования или поиск структуры цифре вой цепи, отличающейся возможностью эффективной программной или аппаратной реализации;

3) реализация цифрового фильтра.

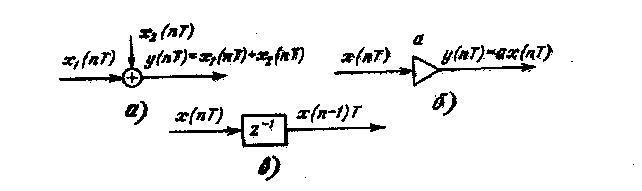
Исходную линейную цифровую цепь представим как совокуп­ность элементарных цифровых звеньев, соединенных друг с дру­гом определенным образом. К числу элементарных цифровых звеньев отнесем сумматор, умножитель на константу и элемент задержки на один период дискретизации Т. Правило, по которому эта цепь отображает воздействие х(пТ) в реакцию у(пТ), обозначим F и назовем оператором цифровой цепи.

Под проектированием линейной цифровой цепи в самом общем случае будем понимать синтез некоторого оператора F, выпол­няющего линейное преобразование пространства сигналов х(пТ) с целью воспроизведения заданной функции передачи , где - приведенная круговая частота, измеряемая в радианах и при­нимающая непрерывные значения в диапазоне . В зависимости от принятой структуры линейной цифровой цепи, которая, в свою очередь, зависит от используемого метода проек­тирования, оператор F имеет различное математическое содержа­ние. Поэтому будем полагать, что различным структурным реали­зациям оператора F соответствуют различные подклассы клас­са операторов , обеспечивающих воспроизведение с наперед за­данной точностью желаемой функции передачи цифровой цепи , представляющей в данном случае комплексную частотную характеристику цепи.

Пространство функций передачи цифровой цепи, строго воспроизводимых в классе операторов G_F, обозначим R. При этом желаемая функция передачи может в общем случае и не принадлежать пространству R. Однако для произвольной должна существовать такая последовательность воспроизводимых в каждом из подклассов функций передачи , при которой для любого сколь угодно малого >0 можно было найти такое n, при котором для всех l>=п имело бы

место неравенство , где —метрика пространства функций R. Иначе говоря, в пространстве R строго воспроизводимых функций передачи должна существовать сходящаяся последовательность, пределом которой является желаемая функция передачи. .

Используя введенные выше понятия и обозначения, задачу проектирования линейно цифровой цепи сформулируем следующим образом: найти подкласс класса операторов G_F и оператор F , такие, что:

где — допустимое отклонение в метрике пространства R.

Если цель проектирования связана не только с воспроизведением заданной функции передачи, но и с оптимизацией некоторого критерия качества (целевой функции) при одновременном выполнении граничных условий ,то задача оптимального проектирования формулируется в виде: найти подкласс класса операторов G_F и оператор F , такие, что:

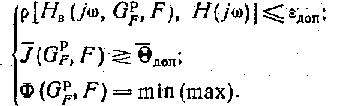
Под оптимальным проектированием цифровой цепи будем понимать, как видно из описания, такое проектирование, которое предполагает не просто поиск оператора, обеспечивающего воспроизведение желаемой функции передачи с заданной точностью, но прежде всего поиск наилучшей в смысле принятого критерия качества структуры цели, включая оптимизацию всех ее параметров.

Рассмотренная выше математическая постановка задачи является достаточно общей и требует конкретизации всех соотношений входящих в формулировку задачи. Возникающие здесь вопросы можно разделить на три группы:

описание и формализация класса операторов G_F обеспечивающих воспроизведение желаемой функции передачи с наперед заданной точностью в метрике пространства R;

описание и формализация подклассов в классе операторов G_F,

представление целевой функции и вектора граничных условий в подклассах в классе операторов G_F.

Рассмотрим постановку и решение задачи аппроксимации с желаемой функцией передачи . Желаемую функцию передачи полосового фильтра представим в виде:

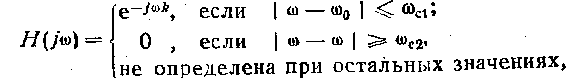
где — Центральная частота полосы пропускании, и частоты среза полосы пропускания и зоны непрозрачности; k — параметр, определяющий постоянную задержки.

Таким образом, будем полагать, что идеальная комплексная частотная характеристика цифрового фильтра частотной селекции должна иметь строго линейную ФЧХ, обеспечивать единичный' коэффициент передачи в полосе пропускания и быть абсолютно непрозрачной в области частот возможного появления помехи.

где р(ш) —весовая функция, принимающая значения

П редставление желаемой частотной характеристики в пространстве R строго воспроизводимых в классе функций пере­дачи является по существу задачей аппроксимации и пред­полагает заданной метрику пространства R. В теории цепей об­щепринятой является минимаксная аппроксимация, решающая за­дачу чебышевского приближения с метрикой вида

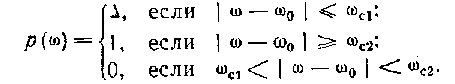- весовая функция, которая обычно принимает вид:

Параметр выбирается из условия