2.19. Адаптивные ких-фильтры. Общее описание и синтез.

Общее описание и методы синтеза.

С целью вывода алгоритма адаптации перейдем от прямой формы свертки отсчетов входного сигнала X(n) и коэффициентов h(k) к векторно-матричной форме представления:

,

где , (5.1)

(5.2)

Мгновенное значение квадрата ошибки:

Пусть , S(n) и X(n) – стационарные эргодические случайные процессы. Найдем средний квадрат отклонения(СКО), представляющий собой мат. Ожидание квадрата ошибки. При этом будем полагать, что на текущем шаге адаптации коэффициенты фильтра принимают постоянное значение.

(5.3)

- корреляционная матрица размером N*N отсчетов входного сигнала

- транспонированный вектор взаимной корреляции обучающего и входного сигнала.

(5.3) фактически описывает так называемую рабочую функцию, определяющую зависимость СКО от выбранного вектора коэффициентов h.

Из (5.2) следует, что если отсчеты входного и обучающего сигнала – стационарные случайные процессы, то рабочая ф-я является квадратичной, при этом СКО, как квадратичная функция имеет только один глобальный оптимум, который легко установить, найдя градиент СКО и приравняв его к 0.

(5.4)

Из (5.4) => (5.5)

Подставив (5.5) в (5.3) получим минимальное значение СКО в точке глобального оптимума.

Принимая во внимание, что матрица R является квадратичной и симметричной, т.е.

, а так же используя правило преобразования матр. произведений и тот факт, что каждой из трех составляющих, входящих в данное выражение, можно показать, что

(5.6)

Анализ выражений (5.5) и (5.6) показывает:

Адаптивная ф-я возможна только при наличии взаисной корреляции входного и обучающего сигнала (а противном случае, если p=0, то Hopt=0).

Должны быть известны корреляционная матрица входного сигнала R и вектор взаимной корреляции P.

Определение оптимального значения вектора коэффициентов связано с необходимостью обращения матрицы R, что при большой размерности вектора коэффициентов N весьма проблематично.

Рассмотрим альтернативный подход, связанный с реализацией градиентных методов поиска экстремума рабочей функции .

Прежде всего отметим, что поскольку рабочая функция является квадратичной, достигающей минимального значения при H=Hopt, то можно ввести следующее представление рабочей функции:

(5.7)

Раскрываем произведение векторов и матриц выражения (5.7) и с учетом (5.6) можно показать, что (5.7) сводится к (5.3), т.е. к исходному уравнению для рабочей ф-ции.

2.20. Адаптивные фильтры. Классификация и применение.

Цифровой фильтр с переменными параметрами преобразующий пространство входных сигналов X(n) в пространство выходных сигналов У(n) с целью воспроизведения желаемой функции передачи назовем адаптивным или фильтром с саморегулированием, если при изменении модели пространства сигналов или цели преобразования он обладает свойствами саморегулирования по заданному критерию качества

z- это цель преобразования

hk(n)- переменные коэффициенты фильтра

Адаптивные фильтры разделяют на два больших класса:

1. Фильтры без ОС ( без предварительного обучения)

2. Фильтры с ОС ( с предварительным обучением)

Фильтры без ОС

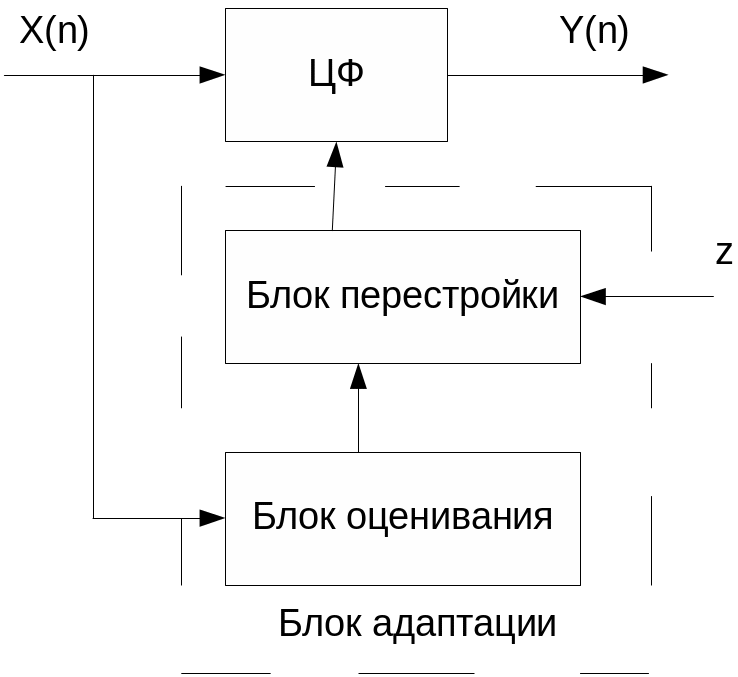
Процесс адаптации без ОС состоит в измерении ( оценивании) характеристик входного сигнала x(n) и в перестройке параметров ЦФ при изменении.

Возможно так же перестройка при смене целей преобразования z.

Процесс адаптации без ОС предполагает что существует и заданы аналитические( алгоритмические) методы синтеза структуры и параметров оператора преобразования F, которые обеспечивают достижение поставленной цели преобразования. Например реализация оптимального Винеровского фильтра по известным корреляционным свойствам сигнала и помехи.