8. Формула полной вероятности. Формула Байеса.

Формула полной вероятности

Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B₁,В₂,.. ., В_п, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: Р (A) = Р (B₁) Р_В1(А) + P (В₂) Р_В2(А)+... +Р(В_п) Р_Вn (А). Эту формулу называют «формулой полной вероятности». Доказательство. По условию, событие А может наступить, если наступит одно из несовместных событийB₁,В₂,.. ., В_п. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий В₁А, В₂А, ..., В_пА, Пользуясь для вычисления вероятности события А теоремой сложения, получим P(A)=P(В₁А)+P(В₂А)+…+P(В_пА). (*) Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем Р (В₁А) = Р (В₁) Р_В1 (А); Р (В₂А) = Р (В₂) Р_В2 (А); ... ;Р (В_nА) = Р (В_n) Р_Вn  (А). Подставив правые части этих равенств в соотношение (*), получим формулу полной вероятности P(A)= Р (В₁) Р_В1 (А)+ Р (В₂) Р_В2 (А)+…+ Р (В_n) Р_Вn (А).

Формула Байеса

Пусть событие A может наступить при условии появления одного из несовместных событий B₁,В₂,.. .,В_п, образующих полную группу.

Тогда Р(В₁/А)= , где Р (А) = Р (В₁) Р_В1 (А)+ Р (В₂) Р_В2 (А)+ ...+ Р (В_n) Р_Вn (А)

Доказательство: По определению условной вероятности, Р(В_I/A)= =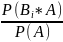

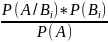
9. Независимые повторные испытания. Формула Бернулли.

Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q=1— p.

Вероятность одного сложного события, состоящего в том, что в n испытаниях событие А наступит k раз и не наступит n—k раз, по теореме умножения вероятностей независимых событий равна p^kq^n-k. Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т. е.  . Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события А в n испытаниях) равна вероятности одного сложного события, умноженной на их число: P_n(k)=

10. Локальная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.

Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р_n (k) того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции

, где

Интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k₁, k₂) того, что событие А появится в п испытаниях от k₁ до k₂ раз, приближенно равна определенному интегралу:

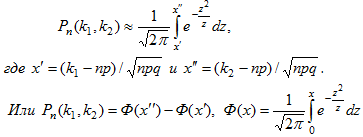 - интегральная функция Лапласа.