
- •Случайные события: виды событий, действия над событиями. Свойства действий над событиями. Отношения между событиями.
- •Частота и относительная частота события. Свойства относительной частоты. Вероятность случайного события. Связь между вероятностью и относительной частотой.
- •Аксиоматическое определение вероятности.
- •Классическое определение вероятности.
- •Геометрическая вероятность.
- •Вероятность суммы событий
- •Условная вероятность случайного события. Вероятность произведения событий. Зависимые и независимые события.
- •Формула полной вероятности. Формула Байеса.
- •Независимые повторные испытания. Формула Бернулли.
- •Локальная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.
- •Дискретная случайная величина: определение, закон распределения, функция распределения. Числовые характеристики дискретной случайной величины.
- •Биноминальное распределение.
- •Распределение Пауссона.
- •Непрерывная случайная величина: определение, функция распределения и ее свойства.
- •Плотность распределения непрерывной случайной величны, свойства плотности распределения.
- •Числовые характеристики непрерывной случайной величины.
- •Равномерное распределение.
- •Нормальное распределение.
- •Двумерная дискретная случайная величина: закон совместного распределения, частные законы распределения компонент. Условные законы распределения компонент. Независимость случайных величин.
- •Свойства математического ожидания случайной величины
- •Свойства дисперсии случайной величины.
- •Числовые характеристики систем случайных величин. Коэффициент корреляции, свойства коэффициента корреляции.
- •Линейная функция регрессии.
- •Неравенство Маркова.
- •Неравенство Чебышева.
- •Теорема Чебышева.
- •Теорема Бернулли.
- •Центральная предельная теорема.
- •Генеральная и выборочная совокупности. Полигон частот ( относительных частот), гистограмма.
- •Выборочная функция распределения.
- •Точечная оценка неизвестных параметров распределения: общая постановка задачи, свойства статистических оценок (несмещенность, состоятельность, эффективность).
- •Выборочная средняя как точечная оценка независимого математического ожидания, свойства.
- •Выборочная дисперсия (определение, свойства), исправленная выборочная дисперсия.
- •Интервальные оценки параметров распределений. Доверительная вероятность и уровень значимости.
- •Проверка статистических гипотез. Общая схема, ошибки первого и второго рода, односторонний и двусторонний критерий, мощность критерия.
- •Сравнение выборочной средней с гипотетической генеральной средней.
Случайные события: виды событий, действия над событиями. Свойства действий над событиями. Отношения между событиями.
Случайными событиями мы будем называть любое явление, которое может происходить вокруг нас (или не происходить).
События называются несовместными, если появление одного из них исключает появление других. Несовместные, т.е. события, которые не могут произойти одновременно.
Теорема: Если события А и В несовместны, то их произведение есть невозможное событие.
Полной группой событий называется совокупность всех возможных результатов опыта.
Достоверным событием называется событие, которое наверняка произойдет в результате опыта.
Событие называется невозможным, если оно никогда не произойдет в результате опыта.
События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.
Действия над событиями.
Суммой А+В двух событий А и В называют событие, состоящее в том, что произойдет либо событие А, либо событие В, либо, если это возможно, они произойдут одновременно.
Произведением А*В событий А и В называется событие, состоящее в том, что события А и В произойдут одновременно.
Разностью А\В событий А и В называется событие, состоящее в том, что произойдет та часть события А, которая не входит в В.
Событие противоположное к данному. А или дополнение события А.
Частота и относительная частота события. Свойства относительной частоты. Вероятность случайного события. Связь между вероятностью и относительной частотой.
Пусть в n опытах некоторое событие А наступило Na раз. Число Na – частота события А.
 P*(A)
- относительная частота (частота).
P*(A)
- относительная частота (частота).
Свойства:
 P*(A)
P*(A)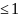
P*( ) = 0
P*(Ω) = 1
Если А и В несовместны, то P*(A+В) = P*(A)+ P*(В)
Вероятность
события А
называют отношение числа благоприятствующих
этому событию исходов к общему числу
всех равновозможных несовместных
элементарных исходов, образующих полную
группу. И определяется формулой:
![]() .
Где Р(А) —
вероятность события A, m —
число благоприятствующих событию A
исходов, n —
общее число возможных исходов.
.
Где Р(А) —
вероятность события A, m —
число благоприятствующих событию A
исходов, n —
общее число возможных исходов.
Определение вероятности не требует, чтобы испытания производились в действительности. Определение относительной частоты предполагает, что испытания были произведены фактически. Или вероятность вычисляют до опыта, а относительную частоту – после опыта.
Аксиоматическое определение вероятности.
Вероятностью события А называется числовая функция Р(А), удовлетворяющая след. аксиомам вероятности:
1. Р(А) ≥ 0 ; неотрицательность
2. Р(Ω) = 1, Ω - достоверное событие ;
3. Для любых попарно несовместных событий А1, А2…An справедливо следующее равенство: Р(A1+A2+…An)=P(A1)+P(A2)+…+P(An)
Следствия из аксиом
1. Вероятность невозможного события равна нулю: P(∅) = 0. 2. Для любого события А P( ) = 1 - P(A). 3. Каково бы ни было случайное событие А, 0 ≤ P(A) ≤ 1. 4. Если событие А влечет за собой событие В, то P(A) ≤ P(B).
5. Р(A1+A2+…An)=P(A1)+P(A2)+…+P(An)
6. P(A+В) = P(A)+ P(В)
