7.2. Барицентрическая система координат на плоскости

На плоскости E² введем дополнительную структуру:

зафиксируем упорядоченную тройку точек, не лежащих на одной прямой: (A₁, A₂, A₃).

Теорема. Для любой точки A плоскости E² существует однозначно определенный набор (l₁, l₂, ₃) такой, что A = l₁A₁ +l₂A₂ +l₃A₃ и ₁ +l₂ +l₃ = 1. Доказательство.

1) Существование набора (l₁, l₂, l₃).

1 случай. Прямая AA₁ не параллельна прямой A₂A₃.

Пусть точка B - точка пересечения прямых AA₁и A₂A₃.

Так как точка A лежит на прямой A₁B, то существует число  такое, что A = (1-) A₁+ B.

Так как точка B лежит на прямой A₂ A₃, то существует число  такое, что B = (1-) A₂+  A₃.

Итак, A = (1-)A₁ + (1-)A₂ + A₃.

Пусть l₁= 1-, l₂ = (1-), l₃= , тогда A = l₁A₁ +l₂A₂ +l₃A₃ и l₁ +l₂ +l₃ = 1.

2 случай. Прямая AA₁ параллельна прямой A₂A₃.

Если прямая AA₂ не параллельна прямой A₁A₃, то повторим доказательство для случая 1, поменяв ролями точки A₁ и A₂.

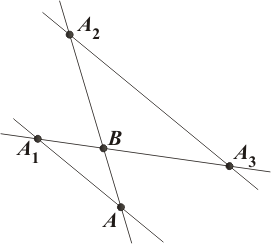
Если прямая AA₂ параллельна прямой A₁A₃, то прямая A A₃ не параллельна прямой A₂A₃, и мы повторим доказательство для случая 1, поменяв ролями точки A₁ и A₃.

РИС.17 (1,2а,2б)

2) Единственность набора (l₁, l₂, l₃).

В п.1 доказательства был предложен способ нахождения набора (l₁, l₂, l₃), докажем, что этот набор (l₁, l₂, l₃) не зависит от способа его получения.

Предположим, что нашелся набор (l₁’, l₂’, l₃’) такой, что A = l₁’ A₁ +l₂ ‘A₂ +l₃ ‘A₃ () и l₁’ +l₂ ‘+l₃’ = 1.

Равенство вида (ð) будем понимать с точки зрения декартовых координат точек.

Итак, A = l₁’ A₁ +l₂ ‘A₂ +l₃ ‘A₃ и A = l₁A₁ +l₂A₂ +l₃A₃.

Тогда (l₁‘ - l₁)A₁ + (l₂‘ - l₂)A₂ +(l₃‘ - l₃)A₃= 0.

Докажем, что l₁‘= l₁, предположим, что это не так, то есть l₁‘-l₁ ≠ 0.

Тогда . Так как , то получается, что точка A₁ делит отрезок [A₂A₃] в отношении , то есть точка A₁ лежит на прямой A₂A₃, что противоречит выбору точек A₁, A₂, A₃.

Следовательно, наше предположение было не верным и l₁‘=l₁.

Аналогично доказывается, что l₂‘= l₂ и l₃‘= l₃.

Определим отображение b: E² ® {(l₁, l₂, l₃) | l₁, l₂, l₃Î R , l₁ + l₂ + l₃ = 1} (ðð) по следующей формуле: b (A) = (l₁, l₂, l₃), если A = l₁A₁ +l₂A₂ +l₃A₃.

Определение. Отображение b (ðð) будем назвать барицентрической системой координат на плоскости.

Определение. Упорядоченный набор (l₁, l₂, l₃) такой, что b(A) = (l₁, l₂, l₃) будем назвать барицентрическими координатами точки A в системе координат b.

Теорема. Отображение b является биективным отображением.

Доказательство. (провести самостоятельно).

7.3. Барицентрическая система координат в пространстве

В пространстве E³ введем дополнительную структуру:

зафиксируем упорядоченную четверку точек, не лежащих в одной плоскости:(A₁, A₂, A₃, A₄).

Теорема. Для любой точки A плоскости E³ существует однозначно определенный набор (l₁, l₂, l₃, ₄) такой, что A = l₁A₁ +l₂A₂ +l₃A₃+ ₄A₄ и l₁ +l₂ +l₃ + ₄ = 1. Доказательство (???самостоятельно ***).

Определим отображение b: E³ ® { (l₁, l₂, l₃, l₄) | l₁, l₂, l₃, l₄ Î R , ₁ +l₂ +l₃ + l₄ = 1} () по следующей формуле: b (A) = (l₁, l₂, l₃, l₄), если A = l₁A₁ +l₂A₂ +l₃A₃ + l₄A₄.

Определение. Отображение b (°) будем назвать барицентрической системой координат в пространстве.

Определение. Упорядоченный набор (l₁, l₂, l₃, l₄) такой, что b(A) = (l₁, l₂, l₃, l₄) будем назвать барицентрическими координатами точки A в системе координат b.

Теорема. Отображение b является биективным отображением.

Доказательство. (провести самостоятельно).