20. Математическое ожидание и его свойства

Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности:  М(Х) = х₁р₁ + х₂р₂ + … + х_nр_n . 

Cвойства математического ожидания

• Математическое ожидание числа есть само число.

,  — константа;

• Математическое ожидание линейно, то есть

, где  — случайные величины с конечным математическим ожиданием, а  — произвольные константы;

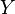• Математическое ожидание сохраняет неравенства, то есть если и  — случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины 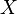также конечно, и более того

;

• Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если , то

.

• Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий

.

21. Дисперсия и ее свойства

Дисперсия случайной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается

Пусть  — случайная величина, определённая на некотором вероятностном пространстве. Тогда

Свойства:

1.ДИСПЕРСИЯ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ РАВНО НУЛЮ.  Пусть а - неслучайная величина. Тогда D(a)=M[(a-M(a))²]=M[0]=0. 2. ДИСПЕРСИЯ СУММЫ НЕСЛУЧАЙНОЙ И СЛУЧАЙНОЙ ВЕЛИЧИН РАВНА ДИСПЕРСИИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ (ДИСПЕРСИЯ ИНВАРИАНТНА СДВИГУ). Пусть а - неслучайная величина. Тогда D(a+x)=M[(a+x-M(a+x))²]= M[(x-M(x))²]=D(x). 3.ДИСПЕРСИЯ ПРОИЗВЕДЕНИЯ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ НА СЛУЧАЙНУЮ РАВНА ПРОИЗВЕДЕНИЮ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НА КВАДРАТ НЕСЛУЧАЙНОЙ ВЕЛИЧИНЫ. Пусть а - неслучайная величина. Тогда D(a*x)=M[(a*x-M(a*x))²]=M[(a*(x-M(x))²]=M[a²*(x-M(x))²]=a²*D(x). 4. ДИСПЕРСИЯ СУММЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН РАВНА СУММЕ ДИСПЕРСИЙ ЭТИХ ВЕЛИЧИН И УДВОЕННОЙ КОВАРИАЦИИ ЭТИХ ВЕЛИЧИН. Пусть x и у - случайные величины. Тогда D(x+y)=M[((x+y)-M(x+y))²]= =M[((x-Mx)+(y-My))²]=M[(x-Mx)²+(y-My)²+2*(x-Mx)*(y-My)]=M[(x-Mx)²]+ +M[(y-My)]+2*M[(x-Mx)*(y-My)]=D(x)+D(y)+2*COV(x,y).  Величина COV(x,y)=M[(x-Mx)*(y-My)] называется ковариацией и обладает свойством: ДЛЯ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН КОВАРИАЦИЯ ВСЕГДА РАВНА НУЛЮ. Отсюда, следует: ДИСПЕРСИЯ СУММЫ ДВУХ НЕЗАВИСИМЫХ (И ТОЛЬКО НЕЗАВИСИМЫХ) СЛУЧАЙНЫХ ВЕЛИЧИН РАВНА СУММЕ ДИСПЕРСИЙ ЭТИХ ВЕЛИЧИН.

22. Нормированные случайные величины

Отклонение случайной величины от ее математического ожидания, иначе говоря, разность между случайной величиной и ее матема­тическим ожиданием называется центрированной случайной ве­личиной

Центрированная случайная величина обладает двумя следующими важными свойствами.

1. Математическое ожидание центрированной случайной величи­ны равно нулю:

2. Дисперсия центрированной случайной величины равна дисперсии самой случайной величины:

Нормированная случайная величина (z) есть центрированная случайная величина, измеренная в масштабе стандартных отклонений : Нормированная случайная величина также отличается двумя свойствами:

Гауссово распределение с произвольными параметрами и определяемое формулой называется общим. Нормированным называют гауссово распределение с параметрами и .

23. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью

где l - положительное число.

прерывное распределение вероятностей случайной величины X, задаваемое плотностью 

 (1)

Плотность р(х).зависит от положительного масштабного параметра l. Формула для моментов:  , в частности - для математич. ожидания   и дисперсии  ; характеристич. функция: (1-it/l)^-1.

П. р. входит в семейство распределений, называемых гамма-распределениями и задаваемых плотностью 

n-кратная свертка распределения (1) равна гамма-распределению с тем же самым параметром lи с a=п. П. р.- единственное распределение, обладающее свойством отсутствия последействия: для любых х>0, у>0 выполняется равенство 

 (2)

где Р{ Х>х+у|Х>у} - условная вероятность события X>x+y при условии X>y. Свойство (2) называется также марковским свойством.