2.3. Модели в системном анализе

Принципиальной особенностью системного анализа является широкое использование на всех этапах методологии моделей систем. Можно сказать, что модель является основным рабочим инструментом системного анализа. В научном понимании модель – это средство отображения реальной системы. Построение модели есть ничто иное, как своеобразный процесс уяснения общих свойств системы и закономерностей ее функционирования и развития, т.е. овладение математическими методами построения моделей систем является необходимым условием овладения методологией системного анализа.

В наиболее общем плане системы можно разделить на реальные (материальные) и абстрактные.

Абстрактные системы представляют собой математические модели реальных систем, отражающие основные свойства этих реальных систем. В дальнейшем абстрактную систему в отличие от реальной будем называть математической моделью системы или просто моделью.

Лекция №3

2. 3. 1. Отношения

Основные определения.

Отношения бывает одноместными (унарными), двухместными (бинарными), трехместными (тренарными) и n-местными ( n-арными).

Важную роль в построении моделей играют бинарные отношения.

Пусть дано счетное множество М, определенное в евклидовом пространстве Еn.

Бинарным отношением R на множестве М называется подмножество декартового произведения множества М на себя.

Следовательно, отношение R представляет собой множество упорядоченных пар <x,y> некоторых элементов множества М. Если x М и y М и данная упорядоченная пара находится в отношении R, то это записывается в виде: xRy, или <x,y> R M*M.

Примеры отношений:

• отношение равенства x=y;

• отношение порядка x>y;

• отношение старшинства, доминирования: x старше y.

Частным случаем отношений являются функции. Пусть отношение F на множестве М таково, что для всякого x M, для которого справедливо соотношение xFy, т.е. каждому элементу x M ставится в соответствие только один элемент y М, определенный этим условием. Такое соотношение называется функцией. Эта зависимость между x и y обозначается y=F(x).

Если рассматривать отношение F на упорядоченных парах <x,y>, где x М, а y L, и если для каждого элемента x М существует единственный элемент y L, определяемый отношением F, то отношение этого вида также называют функцией или отображением и записывают в виде F: – отображение множества M в L.

Бинарное отношение может быть задано в виде:

- матриц;

- графов;

- сечений (окрестностей) единичного радиуса.

При матричном задании бинарного отношения берут двухвходовую матрицу и каждой строке (столбцу) взаимно однозначно сопоставляется элемент множества М, при этом каждое пересечение взаимно однозначно соответствует элементу множества М*М . Если элементы находятся в отношении М, то на пересечении строки и столбца ставится 1.

Например:

M, тогда М*М- квадратная матрица 5*5, т.е. R={<x1,x4>,<x2,x3>,<x2,x4>,<x3,x1>,<x3,x5>,<x4,x3>,<x4,x5>,<x5,x1>,<x5,x2>}

Если первым элементам упорядоченных пар <xi,xj> поставить в соответствие строки матрицы, а вторым – столбцы, то матрица R имеет вид:

x1 x2 x3 x4 x5

В= 0 1 0 1 0 x1

0 0 1 1 0 x2

1 0 0 0 1 x3

0 0 1 0 1 x4

1 1 0 0 0 x5

Матрица В, задающая бинарное отношение т.о. называется матрицей смежности. Другой способ матричного задания отношения R заключается в построении матрицы А, в которой каждому столбцу взаимно однозначно соответствует элемент множества М, строке – пара <xi,xj> R и a=1, если <xj,xk> R

-1, если <xk,xj> R

0, если <xk,xj> R

Матрица А, заданная таким образом, называется матрицей инцидентности. Для данного примера имеет вид

x1 x2 x3 x4 x5

А= 1 -1 0 0 0 <x1,x2>

1 0 0 -1 0 <x1,x4>

0 1 0 -1 0 <x2,x4>

0 1 -1 0 0 <x2,x3>

-1 0 1 0 0 <x3,x1>

0 0 1 0 -1 <x3,x5>

0 0 0 1 -1 <x4,x5>

0 0 -1 1 0 <x4,x3>

-1 0 0 0 1 <x1,x2>

0 -1 0 0 1 <x5,x2>

П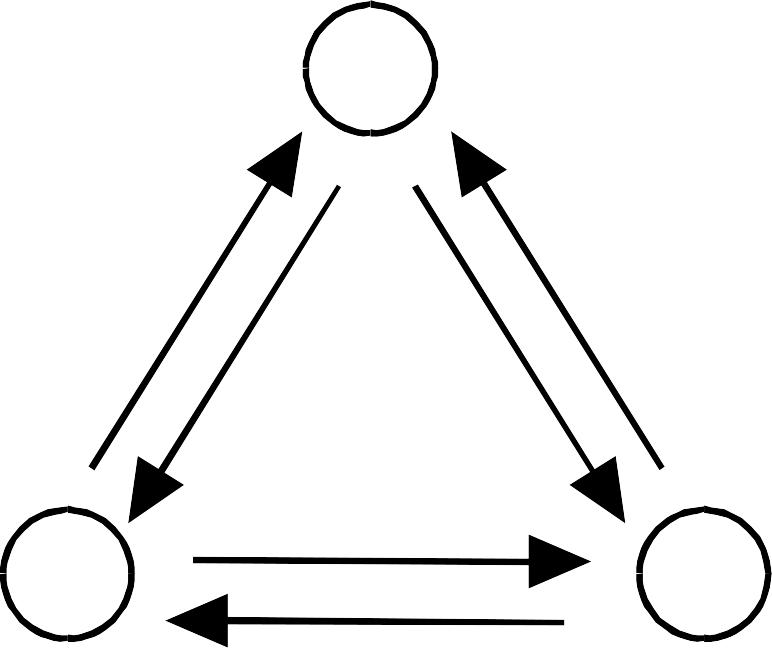 ри задании отношений с помощью графов, элементы множества М изображаются точками, а стрелки, направленные от М характеризуют заданное отношение R.

При задании отношений сечениями, в отличие от предыдущих, возможно задание отношений на бесконечных множествах.

Рассмотрим отношение R на множестве М.

Верхним сечением R+(x) называется множество элементов y М, таких что <y,x> R:

R+(x)={y М/<y,x> R}

Аналогично представляется нижнее сечение: R-(x)={ y М/<х,y> R}