К Лекция № 19

Т.о. получаем кривую безразличия для k₁ Аналогично для k₂. Эта процедура называется Двойная стандартная последовательность. Она позволяет определить лучшую альтернативу для ЛПР. Если кривые пересекаются, то а ~ в.

IV. Методы порогов сравнимости.

Устанавливают отношения на пространстве альтернатив и выявляют эквивалентные альтернативы (“недоминируемые”).

Эта группа методов электра

Существует несколько их видов:

1. Вводятся бинарные отношения.

Имеются k₁, k₂,….k_n – критерии.

Любому критерию можно поставить в соответствие важность: P₁, P₂,….P_n; Для 2-х альтернатив а и в выдвигается гипотеза: а > в. Множество критериев делится на 3 группы:

I⁺ (а, в) - множество критериев, по которым a > в;

I⁼ (а, в) - множество критериев, по которым а = в;

I^- (а, в) - множество критериев, по которым а < в.

Вводится индекс согласия с гипотезой а > в: , , ;

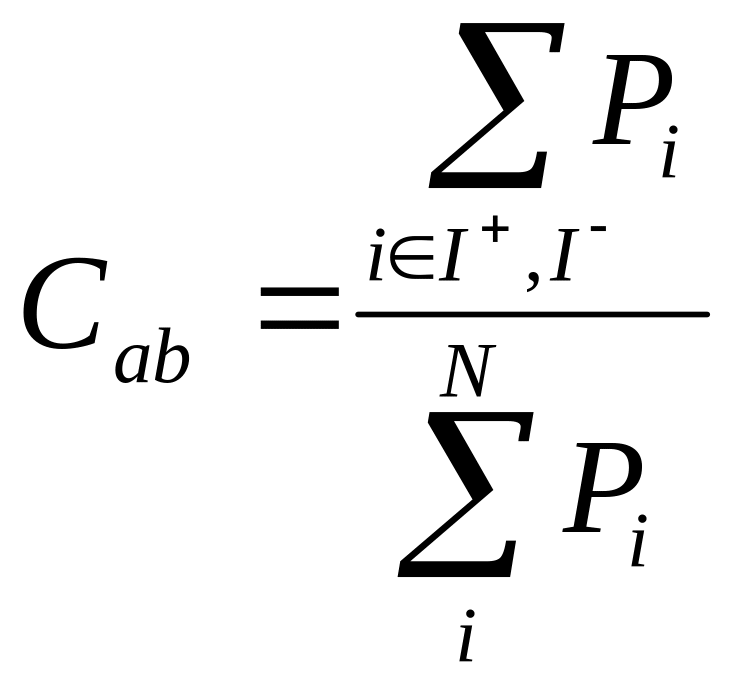Вводится индекс несогласия с гипотезой а > в: для всех критериев берется max разность а и в; обозначим d_ав .

Пусть

Если , где и , то гипотеза а > в принимается.

Меняя с₁ и d₁, можно менять силу превосходства меняем множество недоминирующих альтернатив.

2. Появился добавочный коэффициент.

С_ав считается так же

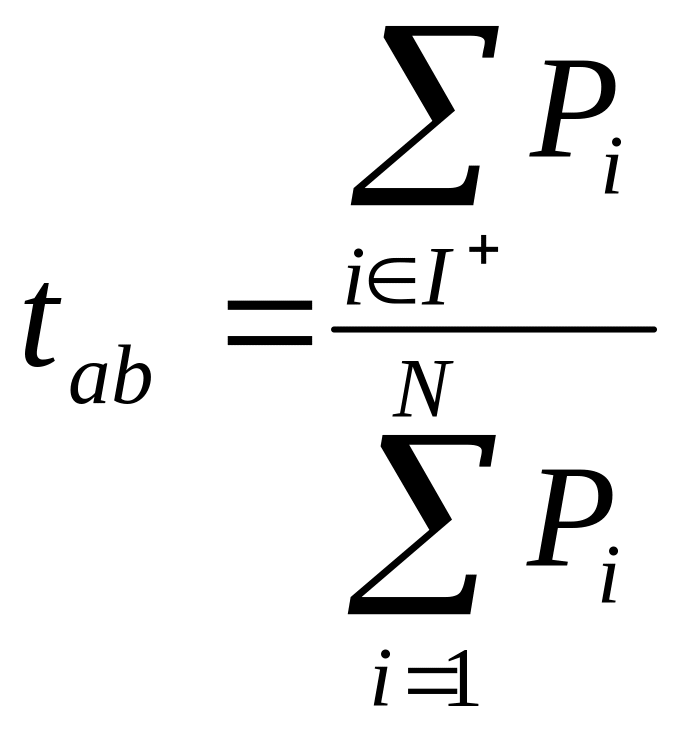
1. индексы согласия и несогласия основанных на нечётких множествах.

Использование нечетких множеств в мкз

- функции принадлежности

Область решения:

Оптимальное решение:

--: вносится субъективизм (функция принадлежности)

Методы прогнозирования Существуют 2 направления:

1. Исследовательское;

2. Нормативное (или антологическое и телеологическое).

1) исследователь не вмешивается в прогноз. Изучается ряд отчетов и выявляется тенденция развития: существует шум, который надо отсеять. Необходимо выбрать математическое описание временного ряда (метод наименьших квадратов). Это экстраполяционные методы.

Были попытки определить такое описание, чтобы отклонения были min-ны – функции с гибкой структурой.

Использовать корреляционные методы: определить связь текущего и прошлого момента (чем дальше в прошлое, тем слабее эта связь) – полином.

К Лекция №20

Зная вид функции, можно определить её коэффициенты. Можно строить регрессионную функцию: - выравнивание через значения в предыдущие моменты.

1) В начале строится корреляционная функция: Частные корреляционные функции – быстрее  к 0.

2) Находим величину

3) Находим коэффициенты по МНК:

4) Находим частое производное u = их к 0

П олучив ряд Z_t, находим Z_t+1,…Z_t+l

2. Эти методы опираются на методологию системного аналитика.

К этим методам относится метод Дельфи:

1) существует некоторая анонимность внесения информации в прогноз;

2) обратная связь;

1. групповой ответ. Прогноз должен п/с число. Члены группы не знают друг друга, указывают цифровую оценку события и теоретическое обоснование этой оценки.

1) ряду определяется медиана и 2 квартиля – верхний и нижний.

Медиана – это число, т.ч. кол-во ответов слева = кол-ву ответов справа (2010).

Нижний Квартиль – это число, которым обладает член ряда под № = ¼ всего ряда.

Верхний Квартиль - это число, которым обладает член ряда под № = ¾ всего ряда.

2) эти 3 числа  экспертам, им даются обоснования других экспертов. Эксперты уточняют свою оценку  новый ряд, более компактный. И т.д. Получается сходящийся ряд.

Существует также морфологический анализ – прогноз облика системы, позволяет определить новые решения (Цвика).

В объекте выделяется набор существенных свойств:

Каждое свойство делится на и нтервалы – состояния:

Р езультат – морфологический ящик.

Р11	Р12	Р13	Р14
Р21	Р22	Р23	Р24

Число N₁

сост-й: N₂

N=N₁.N₂… N₃

- можно комбинировать различные наборы состояний  новый облик системы.

Алгоритм морфологического анализа.

1. задача должна быть чётко сформулирована;

2. должны быть локализированы и проанализированы все свойства, которые имитируют значение для решения;

3. каждое свойство делится на непересекаемые состояния;

4. строится морфологический ящик;

5. обрабатывается и оценивается все варианты с точки зрения поставленных целей.

- : с ростом числа состояний сильно растет N

Используется метод независимых критериев: основанный на предположении, что если можно проранжировать все состояния свойства по важности, то наилучшие варианты будут включать наиболее значимые состояния.

Другой подход – варьирование значений свойств по каждому признаку – методы варьирования по одному признаку: выбирается вариант и фиксируются все свойства кроме одного. Можно ранжировать и сами свойства, менять состояния наименее значимого свойства, затем следующего свойства и т.д. и выбирать оптимальный.