1. Шкала наименований:

Используется для соотношений объектов определенным классам (всем объектам какого-либо класса присваивается одно и тоже число).

К Лекция №8

Эти шкалы допускают взаимно однозначное преобразование: если существуют 2 варианта приписывания классам численных значений, то эти варианты связаны между собой взаимно однозначно. Шкалы наименований не имеют масштаба и начальной точки отсчета.

2) Порядковые шкалы: для упорядочения объектов по одному или нескольким признакам.

R^w=(r|k₁>k₂  r(k₁)>r(k₂)). У этих шкал нет масштаба и начальной точки отсчета.

3) Шкала интервалов: для отображения величины различия между свойствами объектов

П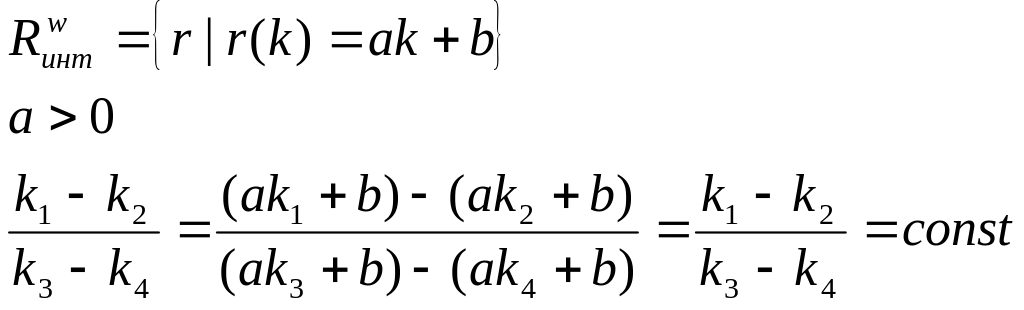 ри преобразованиях различие не изменяется. Например, шкалы Цельсия и Фаренгейта. У этих шкал существует масштаб и начальная точка отсчета.

Т.е сохраняется отношение интервалов.

4) Шкала отношений: для показателей длины, массы, веса – отображает отношения типа: во сколько раз свойство одного объекта превосходит это свойство другого объекта.

Э то частный случай шкалы интервалов, существует масштаб, но нет начальной точки отсчета.

5) Шкала разностей: отражает, насколько один объект превосходит другой объект.

. Существует точка начального отсчета, но нет масштаба.

6) Абсолютная шкала: . Точка отсчета – 0, масштаб – 1, т.е. существует только 1 отображение объекта в числ. систему.

Дерево целей неоднозначно. К решению этой задачи существует 2 подхода:

1. Сверху вниз: Выбирается цели 1-го уровня, затем разбивают каждую из них на подцели и т. д. пока не достигают набор элементарных целей.

2. Снизу вверх: предъявляют набор элементарных целей и надо определить к чему приведет их выполнение.

Этап 3. Разработка альтернатив.

Из всех элементов выделяются наиболее существенные, их связи, проектируется структура системы. Исследуются структурные свойства системы.

Используются методы структурной оптимизации. Критерии оптимальности:

1. Связность графа: наличие висячих вершин.

2. Ранг элемента: исследование элементов с т.з. их значимости в смысле количества вершин, с которыми данная вершина связана.

3. Множество сочленений: исследование графа на совокупность вершин, удаление которых приводит к распаду системы.

Строится функциональная модель системы.

Этап 4. Анализ ресурсов.

Ресурсов должно хватать на весь жизненный цикл (от возникновения идеи до снятия с эксплуатации)

Все ресурсы делятся на:

1. Исследовательские – на создание системы.

2. Производственные – связанные с аппаратной частью.

3. Эксплуатационные – для поддержания системы в рабочем состоянии.

A Лекция №9

В каждой категории надо учитывать различные виды ресурсов: энергетические, материальные, информационные, финансовые и т.д.

Цели этапа “Анализ ресурсов” заключается в выявлении для проектируемой системы:

1. потребных ресурсов по процессам “жизненного цикла”;

2. ограничений по отдельным ресурсам;

3. возможности замещений ограниченных видов ресурсов.

На основании такого анализа разрабатывается модель расходов ресурсов на систему. Обычно при разработке модели расхода ресурсов пользуются стоимостью, как универсальной шкалой измерения ресурсов. Однако для дефицитных видов ресурсов, она м.б. выражена также в натуральном виде. Различают статическую и кинематическую (динамическую) модели расхода ресурсов.

Статическая модель расхода ресурсов разрабатывается в виде матрицы, в которой строки содержат расход ресурсов на подсистему в j- ом процессе жизненного цикла j=1,2,..,n, а столбцы - расход ресурсов за j-ый процесс в i-ой подсистеме.

1 2 … j … n

Т.к. объединение подсистем в систему связано с дополнительными расходами, то суммарный расход ресурсов на систему за процесс составит:

где коэффициент синтеза за j-ый процесс. Расход ресурсов на систему за весь жизненный цикл системы запишется в виде:

В кинематической модели расхода ресурсов процессы жизненного цикла выражены во времени (см. рис.).

С(t)

t

где С(t) – интегральные затраты ресурсов в момент t по всем процессам, - текущие затраты ресурсов в j-ом процессе на момент t.

На основе построения кинематической модели выявляются “пики” в потребных ресурсах, которые при жестких ограничениях на ресурсы могут оказаться существенными для достижения поставленных целей (в заданные сроки).