22. Ранг матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

23. Линейная зависимость и независимость векторов. Ранг системы векторов.

Определение. Если линейная комбинация   может представлять собой нулевой вектор тогда, когда среди чисел   есть хотя бы одно, отличное от нуля, то система векторов   называется линейно зависимой.

Определение.

Если линейная комбинация   представляет собой нулевой вектор только тогда, когда все числа   равны нулю, то система векторов   называется линейно независимой.

Свойства:

1. Если к линейно зависимой системе векторов   добавить несколько векторов, то полученная система будет линейно зависимой.

2. Если из линейно независимой системы векторов   исключить несколько векторов, то полученная система будет линейно независимой.

3. Если в системе векторов   есть хотя бы один нулевой вектор, то такая система линейно зависимая.

4. Если система векторов   линейно зависима, то хотя бы один из ее векторов линейно выражается через остальные. Если система векторов   линейно независима, то ни один из векторов не выражается через остальные.

Из двух последних свойств следует важное утверждение: если система векторов содержит векторы   и  , где   – произвольное число, то она линейно зависима.

Определение. Пусть r – ранг матрицы А порядка p на n,  . Пусть М – базисный минор матрицы А. Все строки (все столбцы) матрицы А, которые не участвуют в образовании базисного минора М, линейно выражаются через строки (столбцы) матрицы, порождающие базисный минор М.

А теперь поясним связь теоремы о ранге матрицы с исследованием системы векторов на линейную зависимость.

Составим матрицу A, строками которой будут векторы исследуемой системы  :

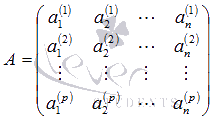
Что будет означать линейная независимость системы векторов  ?

Из четвертого свойства линейной независимости системы векторов   мы знаем, что ни один из векторов системы не выражается через остальные. Иными словами, ни одна строка матрицы A не будет линейно выражаться через другие строки, следовательно, линейная независимость системы векторов   будет равносильна условию Rank(A) = p.

Что же будет означать линейная зависимость системы векторов  ?

Все очень просто: хотя бы одна строка матрицы A будет линейно выражаться через остальные, следовательно, линейная зависимость системы векторов  будет равносильна условию Rank(A) < p.

Итак, задача исследования системы векторов на линейную зависимость сводится к задаче нахождения ранга матрицы, составленной из векторов этой системы.

Следует заметить, что при p > n система векторов   будет линейно зависимой.

Замечание: при составлении матрицы А векторы системы   можно брать не в качестве строк, а в качестве столбцов.

24. Теорема Кронекера - Капелли.

Определение. Матрица (A|B) – расширенная матрица системы.

Теорема. Система имеет решение тогда и только тогда, когда rang(A|B)=rang(A).

Если rang(A|B)=rang(A)=n, то система имеет единственное решение.

Если rang(A|B)=rang(A)=k, где k<n, то система имеет бесконечное множество решений.

Нет решений, если ранги не совпадают.

25. Правило Крамера.

Система линейных уравнений:

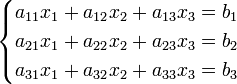
Определители:

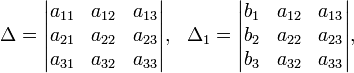
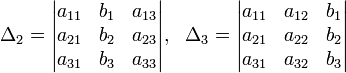
Решение:

26. Метод Гаусса для решения системы линейных уравнений.

Рассмотрим систему из p линейных уравнений с n неизвестными (p может быть равно n): 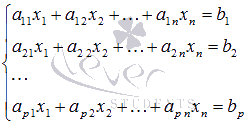  где   - неизвестные переменные,   - числа (действительные или комплексные),   - свободные члены. Если  , то система линейных алгебраических уравнений называется однородной, в противном случае – неоднородной. Совокупность значения неизвестных переменных  , при которых все уравнения системы обращаются в тождества, называется решением СЛАУ. Если существует хотя бы одно решение системы линейных алгебраических уравнений, то она называетсясовместной, в противном случае – несовместной. Если СЛАУ имеет единственное решение, то она называется определенной. Если решений больше одного, то система называется неопределенной. Говорят, что система записана в координатной форме, если она имеет вид . Эта система в матричной форме записи имеет вид  , где   - основная матрица СЛАУ,   - матрица столбец неизвестных переменных,   - матрица свободных членов. Если к матрице А добавить в качестве (n+1)-ого столбца матрицу-столбец свободных членов, то получим так называемую расширенную матрицу системы линейных уравнений. Обычно расширенную матрицу обозначают буквой Т, а столбец свободных членов отделяют вертикальной линией от остальных столбцов, то есть,   Квадратная матрица А называется вырожденной, если ее определитель равен нулю. Если  , то матрицаА называется невырожденной.  Следует оговорить следующий момент. Если с системой линейных алгебраических уравнений   произвести следующие действия: 1. поменять местами два уравнения,

2. умножить обе части какого-либо уравнения на произвольное и отличное от нуля действительное (или комплексное) число k,

3. к обеим частям какого-либо уравнения прибавить соответствующие части другого уравнения, умноженные на произвольное число k,

то получится эквивалентная система, которая имеет такие же решения (или также как и исходная не имеет решений).  Для расширенной матрицы системы линейных алгебраических уравнений эти действия будут означать проведение элементарных преобразований со строками:

1. перестановку двух строк местами,

2. умножение всех элементов какой-либо строки матрицы T на отличное от нуля число k,

3. прибавление к элементам какой-либо строки матрицы соответствующих элементов другой строки, умноженных на произвольное число k.