10. Векторы, линейные операции над ними, свойства этих операций.

Вектор – направленный отрезок.

Сложение векторов   и   происходит так: от произвольной точки A откладывается вектор  , равный  , далее от точки B откладываеься вектор  , равный  , и вектор  представляет собой сумму векторов   и  . Такой способ сложения двух векторов назвается правилом треугольника.

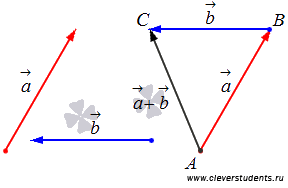
Умножение вектора на число k соответствует растяжению вектора в k раз при k > 1 или сжатию в   раз при 0 < k < 1, при k = 1 вектор остается прежним (для отрицательных k еще изменяется направление на противоположное). Если произвольный вектор умножить на ноль, то получим нулевой вектор. Произведение нулевого вектора и произвольного числа есть нулевой вектор.

Свойства операций над векторами.

1. Свойство коммутативности  .

2. Свойство ассоциативности сложения  .

3. .

4.

5. Сочетательное свойство умножения 

6. Первое распределительное свойство 

7. Второе распределительное свойство 

8.

11. Скалярное произведение двух вектором и его свойства.

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.

Свойства скалярного произведения

1. a •b = b• a;  2. (λa)•b= •(λb) = λ (a•b);  3. a•(b+с) = a•b+a•с;  4. a • a = | a |²;  5. a • b = 0, если a ┴ b.

12. Вычисление скалярного произведения двух векторов, заданных координатами.

Пусть заданы два вектора

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:

   

    т.е

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

13. Векторное произведение двух векторов и его свойство.

Векторным произведением двух векторов   и  , заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор  , что

1. он является нулевым, если векторы   и   коллинеарны;

2. он перпендикулярен и вектору   и вектору   ;

3. его длина равна произведению длин векторов   и   на синус угла между ними ( );

4. тройка векторов   ориентирована так же, как и заданная система координат.

Векторное произведение векторов   и   обозначается как  .

свойства векторного произведения:

1. антикоммутативность  ;

2. свойство дистрибутивности   или  ;

3. сочетательное свойство   или  , где   - произвольное действительное число.

14. Вычисление векторного произведения двух векторов, заданных своими координатами.

В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов   и   есть вектор  , где   - координатные векторы.

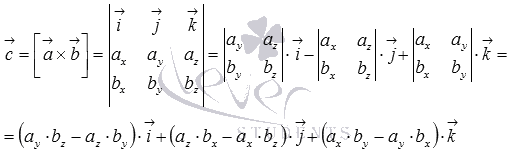
15. Смешанное произведение трех векторов и его свойства; геометрический смысл.

Смешанным произведением векторов   называется число , равное скалярному произведению вектора  на векторное произведение векторов   и  . Смешанное произведение обозначается 

Свойства смешанного произведения:

1. ;

2. ;

3.

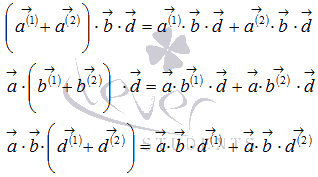
Геометрический смысл:

абсолютная величина смешанного произведения векторов представляет собой объем параллелепипеда:

16. Вычисление смешанного произведения векторов, заданных своими координатами.

Смешанное произведение векторов равно определителю матрицы третьего порядка, строками которой являются координаты умножаемых векторов, то есть, .

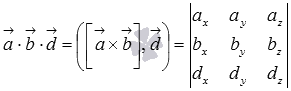Векторное произведение в координатах имеет вид 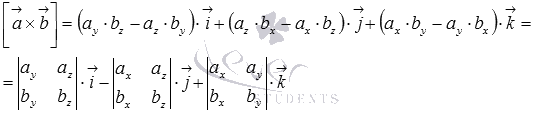  а скалярное произведение векторов в прямоугольной системе координат равно сумме произведений соответствующих координат, поэтому,

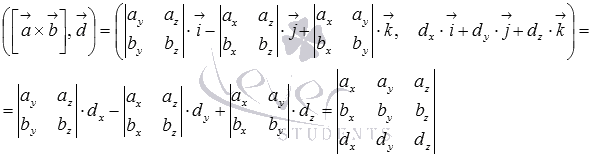
17. Матрица, операции над матрицами.

Матрица – таблица, в частном случае чисел, элементов, состоящая из m строк и n столбцов.

Операции над матрицами:

1. Сложение матриц - поэлементная операция

2. Вычитание матриц - поэлементная операция

3. Произведение матрицы на число - поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ij матрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы B , т.е.

5. Возведение в степень

m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A'

Строки и столбцы поменялись местами