4. Гипербола, ее свойства, каноническое уравнение.

Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

 

 

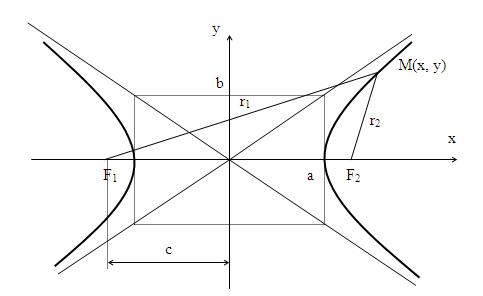
По определению | r 1 – r 2 | = 2 a . F 1 , F 2 – фокусы гиперболы. F 1 F 2 = 2 c .

Выберем на гиперболе произвольную точку М(х, у).

с2 – а2 = b2 (геометрически эта величина – меньшая полуось)

Получили каноническое уравнение гиперболы. Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью.

Ось 2b называется мнимой осью.

Гипербола имеет две асимптоты, уравнения которых 

Определение. Отношение   называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с2 – а 2 = b2

 :

Если а = b , e =  , то гипербола называется равнобочной (равносторонней).

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: 

Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.

Пример 1 . Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса 

Для эллипса: c 2 = a2 – b2 .  Для гиперболы: c2 = a2 + b2 .

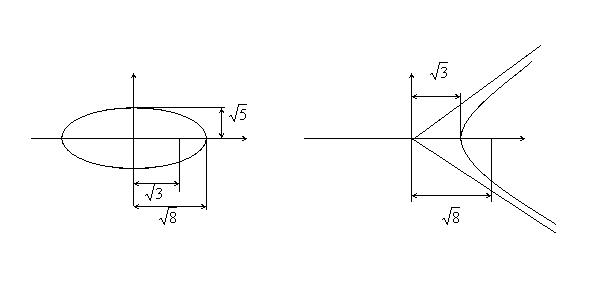
Уравнение гиперболы:

Пример 2 . Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением 

Находим фокусное расстояние c 2 = 25 – 9 = 16.

Для гиперболы: c2 = a2 + b2 = 16, e = c / a = 2; c = 2 a ; c 2 = 4 a2 ; a2 = 4;

b2 = 16 – 4 = 12.

Итого:   - искомое уравнение.

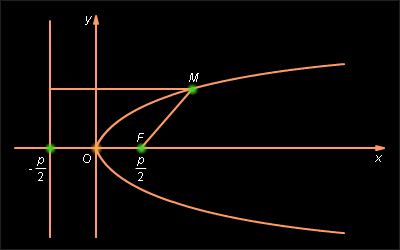
5. Парабола, ее свойства, каноническое уравнение.

Парабола — геометрическое место точек, равноудалённых от

данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Запишем уравнение параболы в новой, канонической системе координат: 

Свойства: 

1. Парабола имеет ось симметрии.

Ось симметрии называется осью параболы. Точка пересечения параболы с осью называется вершиной параболы. Вершина параболы в канонической системе координат находится в начале координат.

2. Парабола расположена в полуплоскости x ≥ 0.

При замене системы координат заданная в условии точка A с координатами   будет иметь новые координаты, определяемые из соотношений 

Таким образом, точка A будет иметь в канонической системе координаты  . Данную точку   называют фокусом параболы и обозначают буквой F.

Прямая l, задаваемая в старой системе координат уравнением   в новой системе координат будет иметь вид 

Данная прямая в канонической системе координат называется директрисой параболы. Расстояние от нее до фокуса называется фокальным параметром параболы. Очевидно, он равен p. Эксцентриситет параболы по определению полагают равным единице, то есть ε = k = 1.

Теперь свойство, через которое мы определили параболу, в новых терминах можно сформулировать следующим образом: любая точка параболы равноудалена от ее фокуса и директрисы.