1. Активы. Финансовые активы. Потоки платежей. Структура финансового рынка. Простые и сложные потоки платежей

• Финансовый актив – вид собственности, имеющий цену, определенную на рынке.

• Материальные активы – имеют физ свойства ( воспроизводимые, невоспроизводимые)

• Нематериальные активы – ПО, патенты, конференции…

• Финансовый инструмент – финансовый актив, имеющий стандартную форму.

• Финансовый рынок : долевые инструменты (право собственности), долговые инструменты (с правом возврата)

• Рынок капитала: долговые инструменты( до 1г, до 10, больше 10), долевые ( акции, привилегии, ADR, GDR), деривативы (фьючерсы, форварды, опционы…)

• Финансовые потоки платежей:

• Стандартный – смена направления финансовых средств происходит не более 1 раза

• Нестандартный – смена направления более 1 раза

• 2 Простые проценты. Сложные проценты. Эффективная процентная ставка. Непрерывно начисляемая процентная ставка. Условие равновесия рынка

• Простые проценты: М= Мо(1+n*r)

• Сложные проценты: М = Мо( 1+R/m)^m*n

• Эффективная процентная ставка: reff=( 1+R/m)^m -1

• Непрерывно начисляемая процентная ставка: ρ=m*ln(1+R/m)

• Условие равновесия рынка: reff1=reff2=reff- const , ρ1=ρ2=ρ – const

• 3 Форвардная процентная ставка. Ставка дисконтирования

• Forward – безусловное обязательство двух сторон в совершении операции купли-продажи ресурсов в определенный момент в будущем в определенном месте по заранее оговоренной цене.

• Forward на депозит: в любой момент времени t1 две стороны продавец – размещает депозит по ставке τ на срок ti, покупатель – обязуется разместить для себя этот депозит: ti+ t =t2,

• V* e^(ρ(τ )* t) – покупатель возвращает продавцу (деньги+%)

• Справедливая форвардная ставка: ρ(F)( t1; t2- t1)

• 4 Настоящая и будущая стоимость денег

• Сегодня…………Т

• 

• Мо Мо

• Если положить в банк:

• М(Т) (будущие деньги) = Мо*e^(ρ*T); M(T)>Mo

• Mo(приведенные деньги) = М (Т)/ e^ (ρ*T)=М (T)*e^(-ρ*T)

• C2 c3 c4

• t1 t2 t3 t4 t5

• c 1 c5

• c1’ = c1*e^(-ρ*T1)

• Ci’ = Ci* e^( -ρ*Ti)

• Po = ∑ci*e^ (-ρ*Ti)

• 5 Рента. Простая рента. Рента с начислениями

• Рента – платеж через фиксированный интервал времени и имеет одинаковую величину.

• Стоимость ренты : Рт=e^(ρ*T) *C*

• P = C* , γ = e^(-ρ* t)

• Вечная рента Т∞ Po = C(m)/ R(m)* 1 -

• n∞ Po= Co*

• e^( α-ρ)/m =

• Po= Co*m*

• a<R(m): Po ≈

• R(m) : Po ≈

• a= R(m): Po=n*Co

• 6. Простой дисконтный вексель

• Простая купонная облигация - ценная бумага, гарантирующая его владельцу получение денег, соотв. номиналу векселя.

• N – номинал

• T – срок до погашения

• N₀ – текущая стоимость

• N<N₀ ; N₀=(1-d)^T*N;

• d – ставка дисконтирования (0<d<1)

• 7.Оценка стоимости ренты

• Рента – платежи через фиксированный интервал времени и имеют одинаковую величину.

• Приведенная стоимость ренты:

• c_i=с

• t_i = i∆t

• 

• P = C

• P₀ = (1 - )

• α – показатель роста ренты

• P₀ = C₀

• 

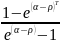
• P₀ = C₀m

• P₀ ~

• P₀ = nC₀

8. Учет инфляции.