3. Пирамида

На рисунке 98 показано пересечение поверхности пирамиды фронтально-проектирующей плоскостью Р. На рисунке 98б изображена фронтальная проекция а точки встречи ребра KS с плоскостью P. Она определяется пересечением следа P_v с фронтальной проекцией ребра k?s? (рис. 98 а). Если фронтальная проекция а? точки А дана, то легко найти её горизонтальную проекцию а.

На рисунке 98, б показаны натуральные размеры ABC сечения ABC, которые были определены совмещением его с горизонтальной плоскостью путем вращения около следа P_h. Отдельно на этом рисунке показаны элементы, которые необходимы для построения развертки. Натуральные размеры ребер пирамиды можно найти путём вращения их около оси, проходящей через вершину S перпендикулярно горизонтальной плоскости, как показано на рисунке 98 в. На рисунке 98 г показана развертка, а изображение каждого из треугольников, входящих в состав развертки, можно построить по трём его сторонам – ребрам.

На рисунке 99 показано пересечение поверхности пирамиды горизонтально-проецирующей плоскостью Q. Треугольник ABC является сечением поверхности пирамиды плоскостью Q, основание АС которого проецируется на горизонтальную плоскость без искажения, а высота BD – на фронтальную и профильную плоскости.

Чтобы построить натуральное изображение сечения, нужно провести через проекции а, с и d вспомогательные прямые, которые перпендикулярны Q_h. После этого следует провести прямую АС параллельно Q_h (AC?аА), точка Dбудет лежать на АС. Затем необходимо отложить от точки D на прямой Dd высоту треугольника (DB = d?b?). Это определит положение вершины В. Теперь треугольник ABC представляет собой натуральный вид сечения поверхности данной пирамиды плоскостью Q. Строить натуральный вид треугольника сечения весьма удобно слева от фронтальной проекции (треугольник ABC).

4. Косые сечения

Под косыми сечениями понимают круг задач на построение натуральных видов сечений рассматриваемого тела проецирующейся плоскостью. Для выполнения косого сечения необходимо расчленить рассматриваемое тело на элементарные геометрические тела, например призму, пирамиду, цилиндр, конус, шар и т. д. После чего следует строить натуральный вид искомого сечения, рассматривая последовательно пересечение плоскости с каждым из этих тел.

На рисунке 100 показана правильная четырёхгранная пирамида с призматическим сквозным отверстием, которая пересечена фронтально-проецирующей плоскостью. Пусть требуется построить натуральное изображение сечения. Она представляет собой две равнобедренные трапеции ABCD и EFGH.

На плане представлены размеры сторон параллельных оснований в натуральную величину, а расстояния между ними, которые являются высотами трапеций, – на главном виде. Для построения сечения этих данных достаточно. Построение выполняют в следующем порядке:

1) проводят ось симметрии сечения параллельно фронтальному следу секущей плоскости, переносят на нее высоты упомянутых трапеций. С этой целью проводят через соответствующие точки следа секущей плоскости прямые, которые перпендикулярны этому следу;

2) откладывают по обе стороны от оси симметрии половины натуральных размеров оснований трапеций:

AD = ad, BC = bc и т. д.;

3) соединяют построенные точки прямыми и заштриховывают полученные площади сечения.

Также натуральный вид сечения можно наблюдать справа от горизонтальной проекции пирамиды (A₁B₁C₁D₁ иE₁F₁H₁).

Заметим, что точки D, С, Н и G лежат на одной прямой, так же как и точки F, Е, В и А на другой прямой. Эти прямые являются сечениями передней и задней граней, каждая из которых разрывается отверстием на две части (это важно при построении натурального вида сечения).

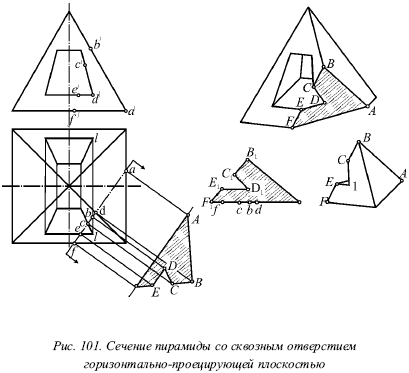
На рисунке 101 показана пирамида, пересеченная горизонтально-проецирующей плоскостью. Пусть требуется построить натуральный вид сечения. Здесь прямую AF можно считать основанием многоугольника сечения, тогда построим это основание и от него будем откладывать высоты остальных вершин сечения. Следует поместить отрезок AF параллельно af, проводя прямые аА и fF перпендикулярно af (AF = af). Затем через горизонтальные проекции (b, с, d и е) остальных вершин многоугольника проводят прямые, перпендикулярные af. Потом откладывают на них по другую сторону от AF высоты перечисленных точек, основываясь на размерах главного вида. При этом отрезок DE должен быть параллельным AF.

Представим, выполняя это построение, что мы как бы совместили сечение с горизонтальной плоскостью проекций, вращая его около горизонтального следа af секущей плоскости, после чего немного отодвинули его в направлении, перпендикулярном следу af.

Также натуральный вид построен справа от фронтальной проекции (A₁B₁C₁D₁E₁F₁).

При этом точки В, С, Е и F лежат на одной прямой.

34. Задачу на построение сечения многогранника (рис. 6), например, пирамиды SABC, плоскостью общего положения сводят к многократному решению задачи на пересечение прямой с плоскостью. Для этого вначале строят вершины многоугольника сечения, как точки пересечения ребер SA, SB и SC многогранника с секущей плоскостью Σ. А затем соединяют отрезками каждые две вершины многоугольника сечения, лежащие в одной и той же грани многогранника.

Рассмотрим решение конкретных задач на построение проекции сечения многогранника плоскостью общего положения.

Рис. 6.

На чертеже (рис. 7, а) изображены треугольная пирамида SABC и секущая плоскость α. Анализируя расположение заданных фигур на чертеже (рис. 7, б), устанавливают, что основание пирамиды — треугольник αBC и прямая h расположены в горизонтальной плоскости проекций, так как их фронтальные проекции совпадают с осью OX.

Это позволяет определить на чертеже положение точек E и F пересечения прямой h, принадлежащей плоскости α, с гранью αBC.

Рис. 7.

Выявив горизонтальные E₁-F₁ проекции точек, строят их фронтальные проекции E₂-F₂. Прямая EF E₁, F₁, E₂, F₂, представляет собой линию пересечения основания пирамиды с плоскостью общего положения.

Далее предполагают, что с секущей плоскостью α пересекаются ребра SA, SB и SC боковой поверхности пирамиды. Проекции прямых SA, SB, SC не параллельны и не перпендикулярны оси проекций OX. Это значит, что каждая из этих прямых занимает в пространстве общее положение.

Тогда для построения проекций вершин сечения боковой поверхности пирамиды необходимо определить положение на чертеже проекций точек пересечения каждой из прямых SA, SB, SC с плоскостью α. Так как эти прямые занимают  общее положение, то для построения проекций точек их пересечения с плоскостью α используют вспомогательные проецирующие плоскости.

На чертеже (рис. 7, в) прямая SA заключена во вспомогательную фронтально-проецирующую плоскость Σ. След  Σ₂ секущей плоскости Σ совпадает с фронтальной проекцией S₂А₂ прямой SA. Прямая 1₂2₂ представляет собой фронтальную проекцию линии пересечения двух плоскостей: заданной α и вспомогательной Σ.

Рис. 7.

Строят горизонтальную проекцию 1₁2₁ линии пересечения плоскостей, на горизонтальной плоскости проекций рассматривают взаимное расположение проекций прямых SA и 12. Горизонтальные проекции 1₁2₁ и S₁A₁ прямых пересекаются в точке 4₁ Фронтальная проекция точки пересечения 4₂ располагается на следе 4₂ вспомогательной секущей плоскости Σ. Точка 4 (4₁; 4₂) является искомой точкой пересечения прямой SA с плоскостью a, так как она принадлежит обеим фигурам: прямой SA, потому что проекции точки 4 расположены на соответствующих проекциях этой  прямой и плоскости α, потому что проекции точки 4расположены на соответствующих проекциях  прямой 12, принадлежащей плоскости a.

Для построения точки пересечения прямой SC с плоскостью α заключают прямую SC во вспомогательную фронтально-проецирующую плоскость q (рис. 7, г).  След θ₂ этой секущей плоскости совпадает с фронтальной проекцией S₂ C₂ прямой  SC.

Прямая 1₂ 2₂ представляет собой фронтальную проекцию линии взаимного пересечения двух плоскостей: заданной  α и вспомогательной  θ. Строят горизонтальную 1₁ 2₁ проекцию линии взаимного пересечения двух плоскостей и на горизонтальной плоскости проекций рассматривают взаимное расположение проекций прямых SC и 12. Горизонтальные проекцuu 1₁ 2₁ и S₁ C₁ прямых пересекаются в точке 5₂.  Фронтальная проекция 5₂ точки пересечения располагается на следе θ₂ секущей плоскости θ.

Точка 5(5₁; 5₂) является искомой точкой пересечения прямой SC и плоскости  α, так как она принадлежит обеим этим фигурам:

прямой SC, потому что  проекции точки 5 располагаются на соответствующих проекциях этой прямой,

плоскости α, потому что проекции точки 5 располагаются на соответствующих проекциях прямой 12, принадлежащей плоскости α.

Для построения точки пересечения прямой SB с плоскостью α    (рис.7, д) заключают прямую во вспомогательную горизонтально-проецирущую плоскость ΦСлед Φ₁ секущей плоскости Φ совпадает с горизонтальной проекцией S₁ B₁ прямой SB. Прямая 1₁ 2₁ представляет собой горизонтальную проекцию линии взаимного пересечения двух плоскостей: заданной α  и  вспомогательной Φ.

Рис. 7.

Строят фронтальную проекцию 1₂ 2₂ линии взаимного пересечения двух плоскостей и на фронтальной плоскости проекций рассматривают взаимное расположение прямых SB и 12. фртальные проекции этих прямых 1₂ 2₂ и S₂ B₂ этих прямых не пересекаются. Это означает, что в пространстве прямая SB не пересекается с плоскостью  α.

Итак (рис. 7, е), в результате выполненных построений выявлены положения проекций вершин — точки  4, 5, F и E  многоугольника, который должен получиться при пересечении пирамиды SABC  с плоскостью  общего положения α.

Попарно соединив отрезками каждые две одноименные проекции точек, лежащих в одной и той же грани многогранника, получают проекции F₁ 4₁ 5₁ E₁ F₁и  F₂ 4₂ 5₂ E₂ F₂ многоугольника сечения пирамиды SABC плоскостью общего положения α, заданной двумя пересекающимися прямыми: фронталью f и горизонталью h.

Решение этой задачи существенно упрощается, если  секущую  плоскость общего положения α преобразовать в проецирующую,  например, способом замены плоскостей  проекций. Для этого на чертеже на горизонтальной плоскости проекций надо провести новую ось проекций  П₁/П₄ перпендикулярно горизонтальной проекции h₁ горизонтали h и построить новую проекцию f₄ фронтали f  (рис. 8). Горизонталь h преобразуется в новой системе плоскостей проекций  П₁/П₄ в точку h₄, расположенную непосредственно на новой оси проекций. Таким образом, в новой системе плоскостей проекций П₁/П₄ плоскость общего положения αявляется проецирующей, так как теперь ее проекция α₄ представляет собой прямую,  совпадающую с проекцией f₄ фронтали f. В новой системе плоскостей проекций П₁/П₄ строят проекции пирамиды S₄ α₄ B₄ C₄

Рис. 8.

Так как проекция S₄, B₄, прямой SB  не пересекается со следом α₄, секущей плоскости  α, то прямая SB в пространстве с плоскостью  α   не пересекается.

Строят проекции 1₄, 2₄, 4₄, 5₄, точек пересечения плоскости  α  с ребрами пирамиды.  Они лежат на пересечении α₄, с проекциями α₄ B₄, B₄ C₄, α₄ S₄, S₄ C₄соответственно. Далее на основании эпюрного признака принадлежности точки прямой линии строят горизонтальные 1₁, 2₁, 4₁, 5₁, а затем фронтальные 1₂, 2₂,4₂, 5₂, проекции этих точек. Для этого необходимо провести линии связи до пересечения с одноименными проекциями ребер αB, BC, αS и SC. Попарно соединив отрезками одноименные проекции точек, лежащих в одной и той же грани, получают проекции 1₁ 4₁ 5₁ 2₁ 1₁ и 1₂ 4₂ 5₂ 2₂ 1₂ многоугольника сечения пирамидыSABC плоскостью общего положения  α.

35.  Прямая пересекает многогранную поверхность в нескольких точках, различных или совпадающих.  Если многогранник выпуклый, то существует 2 точки пересечения прямой с многогранной поверхностью, их называют точками встречи.  Построение точек встречи сводится к решению первой основной позиционной задачи. Рисунок наглядно иллюстрирует решение этой задачи.

Алгоритм построения точек пересечения прямой с многогранной поверхностью: Заключаем прямую a во вспомогательную плоскость . Плоскость  пересекает многогранник по ломаной KLP. Ломаная KLP пересекается с прямой a в точках N и M. Точки N и M – искомые точки пересечения прямой a с многогранником.

 Выбор вспомогательной плоскости  необходимо обосновать в каждом конкретном случае, исходя из точности и простоты построений.