
- •Основные символы
- •§6.1. Множества.
- •5. Открытые полупрямые
- •Вопросы и задания для самопроверки.
- •Упражнения.
- •6. Изобразить на координатной плоскости множества:
- •§6.2. Операции над множествами.
- •Вопросы для самопроверки.
- •Упражнения.
- •§6.3. Модуль числа.
- •Вопросы для самопроверки.
- •Упражнения.
- •2. Решить уравнения:
- •Решить неравенства и изобразить решения на числовой оси:
- •Изобразить на координатной плоскости множества точек, координаты которых удовлетворяют следующим соотношениям:
- •§6.4. Границы числовых множеств.
- •Вопросы и задания для самопроверки.
- •Упражнения.
- •§6.5. Открытые и замкнутые множества.
- •Объединение любого семейства открытых множеств есть открытое множество;
- •Пересечение любого конечного семейства открытых множеств есть открытое множество.
- •Объединение конечного числа замкнутых множеств есть замкнутое множество;
- •Пересечение любого семейства замкнутых множеств есть замкнутое множество
- •Вопросы и задания для самопроверки.
- •Упражнения.
- •§6.6. Первоначальные сведения о функциях.
- •1.Понятие функции.
- •2.Четные и нечетные функции.
- •Если то и , т.Е. Область определения функции f является симметричной относительно начала отсчета о;
- •3.Периодические функции.
- •4.Монотонные функции.
- •Вопросы и задания для самопроверки.
- •§6.7. Обратная функция.
- •Вопросы и задания для самопроверки.
- •Упражнения.
- •Для указанных ниже функций найти обратные функции и построить эскизы их графиков:
- •§6.8. Сложная функция.
- •§6.9. Элементарные функции.
- •Основные формулы для степенных функций.
- •Основные формулы для показательной функции.
- •Логарифмическая функция
- •Основные формулы для логарифмической функции
- •Тригонометрические и обратные тригонометрические функции.
- •Основные значения
- •Основные тригонометрические формулы. Формулы сложения
- •Вопросы и задания для самопроверки.
- •§6.10. Метод математической индукции. Нематематическая индукция играет существенную роль в математическом исследовании.
- •Вопросы и задания для самопроверки.
- •Упражнения.
Вопросы и задания для самопроверки.
Какое множество называется ограниченным сверху (снизу), ограниченным?
Ограничено ли пустое множество?
Всегда ли объединение двух ограниченных множеств есть ограниченное множество?
Всегда ли пересечение двух ограниченных множеств есть ограниченное множество?
Что такое верхняя (нижняя) граница множества?
Приведите примеры ограниченных и неограниченных множеств.
Сколько верхних (нижних) границ имеет множество ограниченное сверху (снизу)?
Верно ли утверждение, что
 ?
Приведите примеры.
?
Приведите примеры.Верно ли утверждение, что
 ?
Приведите примеры.
?
Приведите примеры.Докажите, что множество не может иметь двух различных точных верних (нижних граней).
Назовите свойства точных граней множества.
Может ли точная верхняя (нижняя) граница множества Х принадлежать ему? Приведите примеры.
Может ли верхняя (нижняя) граница множества Х принадлежать множеству Х? Приведите примеры.
Докажите свойства точных границ множества.
Упражнения.
Найдите наибольший и наименьший элементы множества
 .Является
ли число 5 верхней границей множества
.Является
ли число 5 верхней границей множества
 ?
?
Имеет ли множество
 наименьший элемент?, наибольший элемент?
Найдите точные границы этого множества.
наименьший элемент?, наибольший элемент?
Найдите точные границы этого множества.Ограничено ли множество
 ?
Найдите точные границы этого множества.
?
Найдите точные границы этого множества.Имеет ли множество рациональных чисел в промежутке [0, 1) наименьший элемент?, наибольший элемент? Является ли
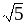 верхней границей множества рациональных
чисел в промежутке [0,
1)?
верхней границей множества рациональных
чисел в промежутке [0,
1)?Ограничено ли множество
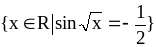 ?
?Ограничено ли множество
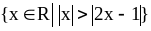 ?
?Найдите точные границы множества
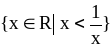 .
.Укажите точные границы множества
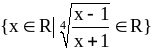 .
.Пусть Х – множество всех рациональных чисел, удовлетворяющих неравенству
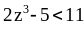 .
Найти sup
X,
inf
X.
.
Найти sup
X,
inf
X.
Решение.
Неравенство
равносильно неравенству
![]() .
Извлекая корень, получим, что
.
Извлекая корень, получим, что
![]() .
Очевидно, наименьшей из верхних границ
будет число 2, т.е.
.
Очевидно, наименьшей из верхних границ
будет число 2, т.е.
![]() .
Так как множество Х неограничено снизу,
то
.
Так как множество Х неограничено снизу,
то
![]() .
.
Найти sup X, inf X, если Х-множество рациональных чисел, удовлетворяющих неравенству
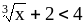 .
.Пусть
 .
Найдите точные границы указанного
множества.
.
Найдите точные границы указанного
множества.
Ограничено ли множество всех целых чисел, делящихся на 3? Ограничено ли оно сверху? Ограничено ли оно снизу?
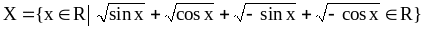 .
Найдите
sup X, inf X.
.
Найдите
sup X, inf X.Ограничено ли множество
 снизу? Ограничено ли оно сверху?
снизу? Ограничено ли оно сверху?
Математика учит точности мысли, подчинению логике доказательств, понятию строго обоснованной истины, а все это формирует личность, пожалуй, больше, чем музыка.
Александров А.Д.
§6.5. Открытые и замкнутые множества.
Всякий
интервал,
содержащий точку а, называется окрестностью
точки а. Окрестность точки а обозначается
О(а). Проколотой
окрестностью
точки а (она обозначается
![]() )
называется любая окрестность О(а) точки
а, из которой удалена точка а. Симметричный
интервал
)
называется любая окрестность О(а) точки
а, из которой удалена точка а. Симметричный
интервал
![]() называется
называется
![]() окрестностью
точки а и
обозначается
окрестностью
точки а и
обозначается
![]() .
Проколотая
окрестность
точки а обозначается
.
Проколотая
окрестность
точки а обозначается
![]() ).
На рисунках интервалы заштрихованы.
).
На рисунках интервалы заштрихованы.
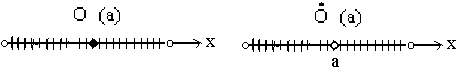
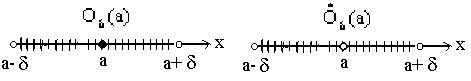
З аметим,
что для конкретной окрестности О(а)
точки а
всегда можно подобрать число
аметим,
что для конкретной окрестности О(а)
точки а
всегда можно подобрать число
![]() (возможно
очень маленькое) такое, что
окрестность
этой точки будет принадлежать О(а).
Справедливо и обратное утверждение,
т.е. во всякой
окрестности
точки а
содержится некоторая окрестность
О(а).
(возможно
очень маленькое) такое, что
окрестность
этой точки будет принадлежать О(а).
Справедливо и обратное утверждение,
т.е. во всякой
окрестности
точки а
содержится некоторая окрестность
О(а).

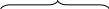
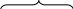

Пусть Х – некоторое непустое числовое множество.
Точка а из множества Х называется внутренней точкой множества Х, если существует некоторая окрестность О(а) этой точки, целиком принадлежащая множеству Х, т.е. .

![]()
Заметим, что окрестность О(а) должна состоять только из точек множества Х.
Так, точка
![]() является внутренней точкой для отрезка
является внутренней точкой для отрезка
![]() ,
так как интервал
,
так как интервал
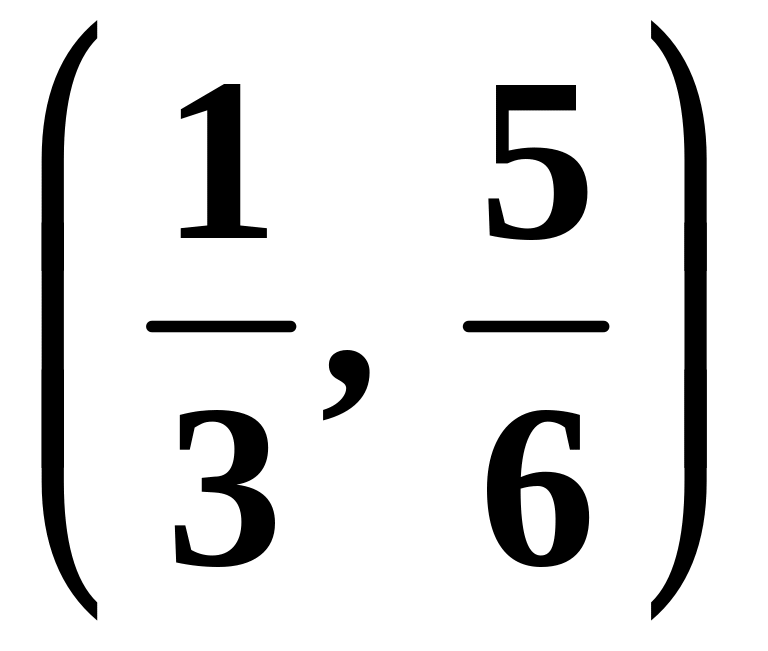 является окрестностью О(
является окрестностью О(![]() )
точки
,
которой принадлежит точка
,
целиком принадлежит отрезку [0, 1].Очевидно,
можно указать бесконечно
много
различных интервалов, содержащих точку
,
каждый из которых будет содержаться
целиком в отрезке [0, 1]. Таким же образом
легко доказать, что каждая точка интервала
(0, 1)
является внутренней
точкой отрезка [0, 1]. Однако, концы отрезка
0 и 1
не являются его внутренними точками. В
самом деле, любой интервал, содержащий
точку 0 (или точку 1) не может целиком
принадлежать отрезку Х
(почему?).
)
точки
,
которой принадлежит точка
,
целиком принадлежит отрезку [0, 1].Очевидно,
можно указать бесконечно
много
различных интервалов, содержащих точку
,
каждый из которых будет содержаться
целиком в отрезке [0, 1]. Таким же образом
легко доказать, что каждая точка интервала
(0, 1)
является внутренней
точкой отрезка [0, 1]. Однако, концы отрезка
0 и 1
не являются его внутренними точками. В
самом деле, любой интервал, содержащий
точку 0 (или точку 1) не может целиком
принадлежать отрезку Х
(почему?).
Множество Х называется открытым множеством, если все его точки являются внутренними точками.
Примером открытого множества может служить интервал (0, 1) или любой другой интервал (a, b). Очевидно, множество всех чисел R является открытым множеством (докажите!). Считается, что пустое множество является открытым. Заметим, что множество (0, 1) является ограниченным открытым множеством, а множество R является открытым, но не ограниченным.Справедлива
Теорема :
