5. Открытые полупрямые

(,a) = {x | xR, <x<a}, (a,+) = {x | xR, a<x<+}.

6. Числовая прямая (,+)=R.

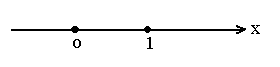
Множество может содержать как конечное число элементов, так и бесконечное. В первом случае множество называется конечным, во втором случае бесконечным. Так, множество государств на Земле конечно, а множество натуральных чисел N бесконечно..

Между двумя множествами установлено взаимно однозначное соответствие, если каждому элементу одного из этих множеств поставлен в соответствие единственный элемент другого множества, и наоборот.

Из этого следует, что двум различным элементам одного из этих множеств соответствуют два различных элемента другого множества. Так, между натуральными числами и четными натуральными числами можно установить взаимно однозначное соответствие, ставя натуральному числу n в соответствие четное число 2n, и наоборот.

Два множества называются эквивалентными , если между ними можно установить взаимно однозначное соответствие. Так множества N и являются эквивалентными.

Множество называется счетным, если оно эквивалентно множеству натуральных чисел.

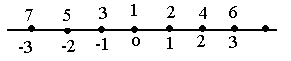
Другими словами, множество счетно, если все его элементы можно пронумеровать. Так, множество всех целых чисел счетно (ниже числовой оси изображены целые числа, а сверху их номера)

Вопросы и задания для самопроверки.

1. Что такое рациональное число? иррациональное число?

2. Может ли быть сумма, произведение, частное двух иррациональных чисел рациональным числом?

3. Что такое пустое множество? конечное множество? бесконечное множество?

4. Приведите примеры конечных и бесконечных множеств.

5. Что такое подмножество данного множества?

6. Назовите все подмножества множества {1,-3, 2, }.

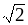7. Может ли множество содержать одинаковые элементы?

8. Какие множества называются равными?

9. Что такое взаимно однозначное соответствие между элементами двух множеств?

10. Существует ли взаимно однозначное соответствие между элементами множества N и элементами множества Z?

11. Какие множества называются эквивалентными?

12. Приведите примеры эквивалентных множеств.

13. Являются ли эквивалентными множества [0,1] и R?

14. Какое множество называется счетным?

15. Приведите примеры счетных множеств.

16. Всякое ли бесконечное множество имеет счетное подмножество?

17. Верно ли, что всякое подмножество счетного множества конечно или счетно?

18. Счетно ли множество рациональных чисел?

19. Соизмеримы ли высота правильного треугольника с его стороной, если сторона равна 1?

20. Установите взаимно однозначное соответствие между множествами [0, 1] и [a, b]; [0, 1] и [0, ).

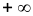Упражнения.

1. Доказать, что число + является иррациональным числом.

Решение.

Предположим противное, т.е., что число + является рациональным. Тогда число - = будет также рациональным, как частное двух рациональных чисел 1 и + . Отсюда вытекает, что число = ( + ) - ( - ) является рациональным, как разность двух рациональных чисел, что противоречит иррациональноти числа . Значит, наше предположение ложно, и число + есть иррациональное число.

2. Доказать иррациональность чисел:

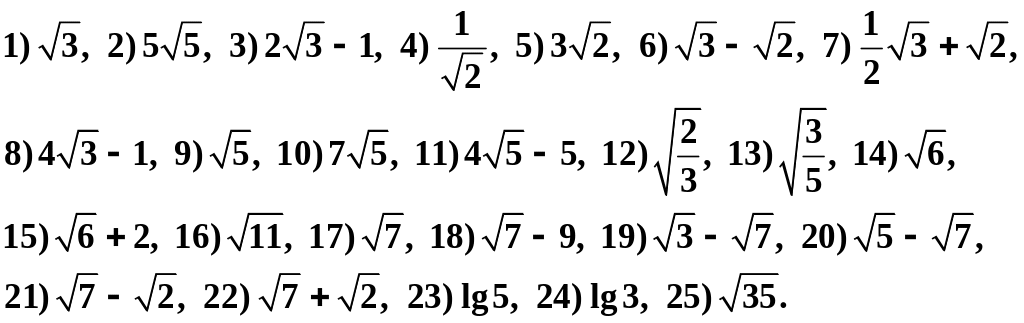
3. Сравните числа:

1) - и - 2, 2) - и - 2, 3) - 1 и - 2,

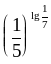4) - и 2 - , 5) и , 6) и , 7) и .

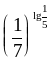4. Установите, какие из записей верны:

1) {3,4}{3,4,{1,3,4}}, 2) {3,4}  {3,4,{1,3,4}},

3) {5,7}{1,2,{5,7,},-3}, 4) {5,7} {1,2,{5,7,},-3}.

5. Описать указанные множества перечислением всех их элементов:

1) {xR | x² -5x+6=0}, 2) {xR | x² -5x+60}, 3) {xR | x² -5x+6<0},

4) {xR | x² -7x+6x}, 5) {xR | (x-1)(x-2)(x-3)0}, 6) {xR | 1},

7) {xR | }, 8) {xR | 0}, 9) {xR | x³ -3x² +2x=0},

10) {xZ | 15}, 11) {xZ | 2}, 12) {xR | sin² x= },

13) {xR | }, 14) {xR | x=sin x}, 15) {xR | x },

16) {xQ | sin x cos x=1}, 17) {(x,y)R² | (x² -1)(y+2)=0}, 18) {(x,y) | x² +y² 5}, 19) {(x,y)R² | sin² x+cos¹⁰ y=2}, 20) {(x,y)R² | sin² x-3sinx+2=0},

21) {xR | }, 22) {xZ | x² }, 23) {xZ | lg(x-3)+3lg2=lg(3x+1)}, 24) {xN | }, 25) {xN | }.