Попередні перетворення опису схем для синтезу схем.
Синтез тестов цифровых устройств является одной из классических задач диагностики вычислительной техники (ВТ), радиоэлектронной и электронно-вычислительной аппаратуры. Но, не смотря на это, она остается практически нерешенной к настоящему времени. Это объясняется, прежде всего, разными темпами развития теории диагностирования и прогрессом ВТ. В последнее время появилось новое направление – контролепригодное проектирование (КПП - desіgn for testabіlіty). Основной характеристикой такого направления является то, что уже на этапе проектирования устройства в него закладываются функции тестирования. Это в свою очередь, обеспечивает снижение трудоемкости при разработке диагностического обеспечения и в первую очередь при синтезе тестов. В данное время, диагносты и ведущие производители ВТ уделяют этому направлению первостепенное внимание, вследствие чего, в этой области достигнут значительный прогресс, как в теоретическом, так и в практическом плане.
С другой стороны, в странах СНГ, в том числе и на Украине, парк ВТ на промышленных и оборонительных предприятиях характеризуется доминированием старых технологий. Приобретение же современных систем, с функциями самотестирования, остается неразрешимой проблемой, прежде всего по экономическим причинам. Поэтому тема данной магистерской работы, направленная на разработку подсистемы синтеза тестов цифровых типовых элементов замены (ТЭЗ), является актуальной задачей.
Одним из направлений построения тестов является случайное (псевдослучайное) тестирование, которое обеспечивает достаточно быстрое построение системы тестов. Но оно имеет большой недостаток - это низкая полнота тестов сложных объектов диагностики (ОД). Поэтому, было принято решение остановиться на детерминированном синтезе тестов, которое обеспечивает высокую полноту теста, но является более медленным. Основные усилия в данной работе как раз и направлены на преодоление этого недостатка - повышение эффективности синтеза тестов.
АОВТ
Двійкова і двійково-кодована система числення.
Системой счисления (Numeration system) называют совокупность правил изображения чисел цифровыми знаками. Исторически сложилось два типа систем счисления – непозиционные и позиционные системы счисления.
При использовании двоичной системы счисления основание которой d=2, для обозначения цифр в разрядах необходимо только два символа 0 и 1. В данном случае представление чисел состоит только из нолей и единиц. При этом, например, запись 1101,1012 соответствует в десятичной системе следующему числу:
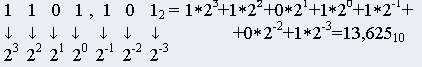
Двоично-кодированную десятичную систему счисления и просто двоичную систему нельзя считать равнозначными, так как одна и та же последовательность нолей и единиц в обеих системах обозначает разные по значению числа. Кроме того, максимальное двоичное число в тетраде двоично-кодированной десятичной системы составляет 1001, что соответствует цифре 9 десятичной системы.
Представлення числової інформації в еом.
Существуют два основных формата представления чисел в памяти компьютера. Один из них используется для кодирования целых чисел, а второй для кодирования действительных чисел. Целые числа представляются в формате с фиксированной запятой, а действительные - в формате с плавающей точкой. Мы с вами уже говорили о том, что алфавит компьютера состоит всего лишь из двух знаков: 0 и 1. Все числа в компьютере и представляются с помощью этих двух знаков. Если говорить о том, как мы с вами записываем числа, то легко заметить, что мы это делаем всего лишь с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Например, число 234 означает, что в числе 2 сотни, 3 десятка и 4 единицы:
234=2*102+3*101+4*100
Другими словами, мы с вами работаем с числами в позиционной системе счисления и представляем число как сумму цифр умноженных на соответствующую степень десяти, то есть в десятичной системе счисления. Компьютер же работает с числами, записанными в двоичной системе. В этой системе счисления всего лишь две цифры: 0 и 1, а числа записываются по степеням двойки. Например, число пять кодируется как 101, потому что
5=1*22+0*21+1*20=1012
Нижний индекс 2, показывает, что речь идет о двоичной системе счисления. Полезно запомнить, как представляются в двоичной системе десятичные цифры.
Каждый регистр арифметического устройства компьютера, каждая ячейка памяти представляет собой совокупность однородных элементов, каждый из которых может принимать два состояния и используется для записи соответствующего разряда числа. Нумерацию разрядов в ячейке принято вести справа налево.
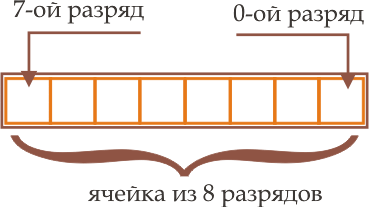
Положительные (беззнаковые) числа представляют во всех разрядах ячейки. Для представления целого числа со знаком используют все разряды ячейки, кроме старшего. Если в старшем разряде расположена 1, то число имеет знак минус, а если 0, то знак - плюс. . Отметим, что отрицательные числа в компьютере представляются дополнительным кодом. Более подробно о компьютерном представлении чисел можно прочитать в четвертой теме данного учебника.
Вещественные числа представляются в компьютере в нормализованной (экспоненциальной) записи , при этом часть ячеек отводится под мантиссу, а часть под порядок. Более подробно о представлении чисел можно прочитать в четвертой теме данного учебника.