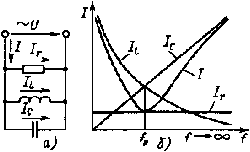21. Резонанс напряжения и тока в электрических цепях

явление резонанса, т. е. совпадения частоты свободных колебаний ?₀, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ?, сообщаемых этой системе внешними силами.

Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ? источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ?₀, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.

РЕЗОНАНС НАПРЯЖЕНИЙ

В общем случае под резонансом электрической цепи понимают такое состояние цепи, когда ток и напряжение совпадают по фазе, и, следовательно, эквивалентная схема цепи представляет собой активное сопротивление. Такое состояние цепи имеет место при определенном соотношении ее параметров r, L, С, когда резонансная частота цепи равна частоте приложенного к ней напряжения.

Резонанс вэлектрической цепи сопровождается периодическим переходом энергии электрического поля емкости в энергию магнитного поля индуктивности и наоборот.

При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и напряжения на отдельных ее участках. В цепи, где r, L, С соединены последовательно, может возникнуть резонанс напряжений, а в цепи, где r, L, С соединены параллельно,— резонанс токов.

Рассмотрим явление резонанса напряжений на примере цепи рис. 2.11, а.

Как отмечалось, при резонансе ток и напряжение совпадают по фазе, т. е. угол φ = 0. и полное сопротивление цепи равно ее активному сопротивлению.

z = √r² + (x_L - x_С)² = r.

Это равенство, очевидно, будет иметь место, если x_L = х_С , т. е. реактивное сопротивление цепи равно нулю:

x = x_L — x_С = 0.

Выразив x_L и x_С соответственно через L, С и f, получим

2πfL =	1	,
	2πfC

откуда

f =	1	= fрез
	2π√LC

где f — частота напряжения, подведенного к контуру; f_рез — резонансная частота.

Таким образом, при x_L = x_С в цепи возникает резонанс напряжений, так как резонансная частота равна частоте напряжения, подведенного к цепи.

Из   выражения   закона   Ома  для   последовательной   цепи

I =	U	.
	√r2 + (xL - xС)2

Рис. 2.14. Векторная диаграмма (а) и графики мгновенных значений и, i, р (б) цепи рис. 2.11, а при резонансе напряжений

вытекает, что ток в цепи при резонансе равен напряжению, деленному на активное сопротивление:

I = U/r.

Ток в цепи может оказаться значительно больше тока, который был бы при отсутствии резонанса. При резонансе напряжение на индуктивности равно напряжению на емкости:

Ix_L = Ix_С = U_L = U_C.

При больших значениях x_L и х_C относительно r эти напряжения могут во много раз превышать напряжение сети. Резонанс в цепи при последовательном соединении потребителей носит название резонанса напряжений.

Напряжение на активном сопротивлении при резонансе равно напряжению, приложенному к цепи:

U_r = Ir = U.

На рис. 2.14, а изображена векторная диаграмма цепи рис. 2.11, а при резонансе напряжений Диаграмма подтверждает тот факт, что ток совпадает по фазе с напряжением сети и что напряжение на активном сопротивлении равно напряжению сети. Реактивная мощность при резонансе равна нулю:

Q = Q_L - Q_C = U_LI - U_CI = 0.

так как U_L = U_C.

Полная мощность равна активной мощности;

S = √P² + Q² = P,

так как реактивная мощность равна нулю. Коэффициент мощности равен единице:

cos φ = P/S = r/z = 1.

Поскольку резонанс напряжений возникает, когда индуктивное сопротивление последовательной цепи равно емкостному, а их значения определяются соответственно индуктивностью, емкостью цепи и частотой сети,

xL = 2πfL,   xС =	1	.
	2πfС

Резонанс может быть получен или путем подбора параметров цепи при заданной частоте сети, или путем подбора частоты сети при заданных параметрах цепи.

На рис. 2.14, б изображены графики мгновенных значений тока i, напряжения и сети и напряжений и_L , и_C , и_r на отдельных участках, а также активной р = iu_r и реактивной p_L= iи_L ,  p_С = iи_С мощностей за период для цепи рис. 2.11. а при резонансе напряжений. С помощью этих графиков можно проследить энергетическне процессы, происходящие в цепи при резонансе напряжений.

Активная мощность р все время положительна, она поступает из сети к активному сопротивлению и выделяется в нем в виде тепла. Мощности p_L и р_С знакопеременные, и, как видно из графика, их средние значения равны нулю.

В момент времени t = 0 (точка I на рис. 2.14, б) ток в цепи i = 0 и энергия магнитного поля  W_L = 0. Напряжение на емкости равно амплитудному значению U_тС, конденсатор заряжен и энергия его электрического поля

WC =	U2тcС	.
	2

В первую четверть периода, в интервале времени между точками 1 и 2, напряжение на емкости и, следовательно, энергия электрического поля убывают. Ток в цепи и энергия магнитного поля возрастают.

В конце первой четверти периода (точка 2) и_С = 0, W_С = 0. i = I_m,  W_L = I²_mL/2.

Таким образом, в первую четверть периода энергия электрического поля переходит в энергию магнитного поля.

Так как площади p_С(t) и p_L(t) , выражающие запас энергии соответственно в электрическом и магнитном  полях, одинаковы, вся энергия электрического поля конденсатора переходит в энергию магнитного поля индуктивности. Во вторую четверть периода, в интервале между точками 2 и 3, энергия магнитного поля переходит в энергию электрического поля.

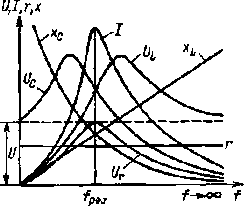
Рис. 2.15. Графики зависимости I, r, хC, хL, Ur, UL , UC от частоты цепи, изображенной на рис  2.11, а

Аналогичные процессы происходят и в последующие четверти периода.

Таким образом, при резонансе реактивная энергия циркулирует внутри контура от индуктивности к емкости и обратно. Обмена реактивной энергией между источниками и цепью не происходит. Ток в проводниках, соединяющих источник с цепью, обусловлен только активной мощностью.

Для анализа цепей иногда используют частотный метод, позволяющий выяснить зависимость параметров цепи и других величин oт частоты.

На рис 2.15 изображены графики зависимости U_r, U_C, U_L , I, х_C , х_L , от частоты при неизменном напряжении сети.

При f = 0 сопротивления x_L = 2πfL = 0, х_C = 1/2πfC = ∞, ток I = 0, напряжения U_r = I_r = 0,  U_L = Ix_L= 0, U_C = U.  При f = f_pез х_L = х_C , I = U/r, U_L = U_C, U_r = U. При f→ ∞ x_L→∞, х_C→ 0, U_r → 0, U_C → 0, U_L → U.

В интервале частот от f = 0 до f = f_pез нагрузка имеет активно-емкостный характер, ток опережает по фазе напряжение сети. В интервале частот f = f_pез до f→ ∞ нагрузка носит активно-индуктивный характер, ток отстает по фазе от напряжения сети.

Наибольшее значение напряжения на емкости получается при частоте, несколько меньшей резонансной, на индуктивности - при частоте, несколько большей резонансной.

Явления резонанса широко используются в радиоэлектронных устройствах и в заводских промышленных установках.

РЕЗОНАНС ТОКОВ

общий ток цепи совпадает по фазе с напряжением, если реактивные составляющие токов ветвей с индуктивностью и емкостью равны по модулю:

I_1р = I_2р.

Общий реактивный ток цепи, равный разности реактивных токов ветвей, в этом случае равен нулю:

I_1р - I_2р = 0.

Общий ток цепи имеет только активную составляющую, равную сумме активных составляющих токов ветвей:

I_а = I_1а + I_2а .

Выразив реактивные токи через напряжения и реактивные проводимости, получим

Ub_L = Ub_С,

откуда

b_L = b_С.

Итак, при резонансе токов реактивная проводимость ветви с индуктивностью равна реактивной проводимости ветви с емкостью.

Выразив b_L и b_С через сопротивления соответствующей ветви, можно определить резонансную частоту контура:

xL	=	xC	=	2πfL	=	1 2πfC	,
r12+ xL2		x22 + xC2		r12 + (2πfL)2		r22+ ( 1 )2 2πfC

откуда

fрез =	1	√	L/C - r12	.
	2π√LC		L/C - r22

В идеальном случае, когда r₁ = r₂ = 0,

fрез =	1	.
	2π√LC

При резонансе токов коэффициент мощности равен единице:

cos φ = 1.

Полная мощность равна активной мощности:

S = P.

Реактивная мощность равна нулю:

Q = Q_L - Q_C = 0.

Энергетические процессы в цепи при резонансе токов аналогичны процессам, происходящим при резонансе напряжений, которые были подробно рассмотрены в § 2.12.

Реактивная энергия действует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода энергия электрического поля емкости переходит в энергию магнитного поля индуктивности. Обмена реактивной энергией между потребителями цепи и источником питания не происходит. Ток в проводах, соединяющих цепь с источником, обусловлен только активной мощностью.

Рис.  2.19.  Электрическая  цепь  (а) и  графики  зависимости   Ir, IL, IC и Iот частоты f (б)

Для резонанса токов характерно, что общий ток при определенном сочетании параметров цепи может быть значительно меньше токов в каждой ветви. Например, в идеальной цепи, когда r₁ = r₂ = 0 (см. рис. 2.18, а), общий ток равен нулю, а токи ветвей с емкостью и индуктивностью существуют, они равны по модулю и сдвинуты по фазе на 180°. Резонанс в цепи при параллельном соединении потребителей называется резонансом токов.

Резонанс токов может быть получен путем подбора параметров цепи при заданной частоте источника питания или путем подбора частоты источника питания при заданных параметpax цепи.

Представляет интерес влияние частоты источника питания на значения токов в цепи, например в цепи, изображенной на рис. 2.19, а.

Ток  в  ветви  с индуктивностью  обратно   пропорционален частоте:

I_L = U/2πfL,

а ток в ветви с емкостью прямо пропорционален частоте:

I_С =U2πfC.

Ток в ветви с активным сопротивлением не зависит от частоты ¹:

I_r = U/r.

Вектор общего тока в цепи равен геометрической сумме векторов токов ветвей:

Ī =Ī_r + Ī_L+Ī_С,

¹ Если пренебречь влиянием вытеснения тока к поверхности проводника.

а значение тока

I = √I_r²+ (I_L - I_C)².

При f = 0

I_L = ∞;    I_C = 0;    I_r = U/r;    I = ∞.

При f = f_рез

I_L = I_C;   I = I_r = U/r.

При f → ∞

I_L → 0;    I_C → ∞;    I_r = U/r;    I → ∞.

Графики зависимости I_r, I_L, I_С и I от частоты изображены на рис. 2.19, б.

Большинство промышленных потребителей переменного тока имеют активноиндуктивный характер; некоторые из них работают с низким коэффициентом мощности и, следовательно, потребляют значительную реактивную мощность. К таким потребителям относятся асинхронные двигатели, особенно работающие с неполной нагрузкой, установки электрической сварки, высокочастотной закалки и т. д.

Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов.

Реактивная мощность конденсаторной батареи уменьшает общую реактивную мощность установки, так как

Q = Q_L - Q_C ,

и тем самым увеличивает коэффициент мощности.

Повышение коэффициента мощности приводит к уменьшению тока в проводах, соединяющих потребитель с источником энергии, и полной мощности источника.