23. Определение видимости элементов фигур на чертеже (конкурирующие точки).

Метод конкурирующих точек используется в начертательной геометрии для определения взаимной видимости двух геометрических фигур.

Конкурирующими точками называются такие точки пространства, у которых совпадают какие-либо две одноименные проекции. 

Метод конкурирующих точек заключается в определении взаимной видимости точек по их несовпадающим проекциям.

Методом конкурирующих точек пользуются при определении видимости пересекающихся геометрических фигур.

 Общее правило. Видимость для совпадающих проекций конкурирующих точек определяется сравнением координат этих точек в направлении общего проецирующего луча. Видима та проекция точки, у которой эта координата больше. При этом сравнение координат ведется на плоскости проекций с раздельными изображениями точек.

  Задача определения видимости конкурирующих точек имеет большое практическое значение. Поскольку окончательная обводка чертежа геометрической фигуры производится с учетом видимости её элементов.

24. Развертки многогранников.

Развертка многогранника представляет собой плоскую фигуру, полученную при совмещении всех его граней с плоскостью. Следовательно, построение развертки многогранника сводится к построению истинных величин его граней. Выполнение этой операции связано с определением натуральных величин его ребер, которые являются сторонами многоугольников – граней, а иногда и некоторых других элементов. Ребра многогранника условно разделяются на боковые и стороны основания. Существуют три способа построения разверток многогранных поверхностей:

1) способ треугольников (триангуляции); 2) способ нормального сечения; 3) способ раскатки.

26. Построение развертки сферы.

Сферическая поверхность является неразвертывающейся. Существующие методы построения ее развертки дают лишь приближенные результаты.

Сущность одного из них заключается в том, что элемент сферической поверхности заменяется элементом цилиндрической поверхности касательной к сфере по главному меридиану m. Ось такой цилиндрической поверхности проходит через центр сферы перпендикулярно G_2.При этом под элементом сферы понимают часть ее, ограниченную двумя большими окружностями.

Для выполнения построения развертки поверхность сферы:

1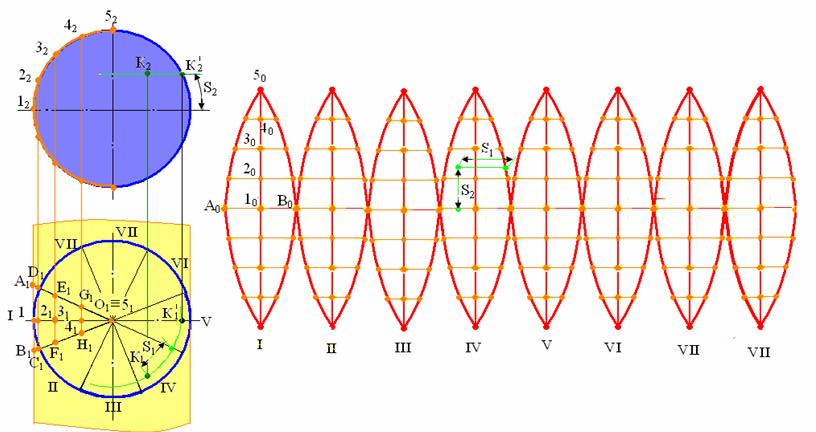 ) разделить большими окружностями на несколько (например 6) равных частей. Каждый из образовавшихся элементов сферы проецируется на плоскость П₁, в виде сектора;

2) описать вокруг сферы цилиндрическую поверхность, ось которой проходит через центр сферы перпендикулярно к П₂;

3) заменить элемент сферы частью цилиндрической поверхности. Горизонтальной проекцией этого цилиндрического элемента окажется треугольник А₁В₁О₁, а фронтальной – контур сферы (дуга окружности).

4) для построения развертки цилиндрического элемента (лепестка) разделить его фронтальную проекцию на восемь равных частей;

5) построить горизонтальные проекции образующих, соответствующих точкам деления. Истинные длины отрезков образующих для построения развертки взять с горизонтальной проекции (отрезки А₁ В₁, С₁ D₁, E₁ F₁, G₁ H₁) а расстояния между ними измерить на фронтальной проекции (расстояния между точками 1₂2₂, и 2₂3₂);

6) при построении цилиндрического элемента (лепестка) через середину отрезка АВ = А₁В₁ провести вертикальную ось симметрии лепестка на которой отложить вверх и вниз четыре отрезка 1₀ –2₀ = 1₂2₂, 2₀ – 3₀ = 2₂3₂, 3₀ – 4₀ = 3₂4₂, 4₀ – 5₀ = 4₂5₂.

7) через точки 2₀, 3₀, 4₀ провести отрезки C₀D₀ = C₁D₁, E₀F₀, G₀H₀ = G₁H₁.

8) соединить плавной кривой концы отрезков, в результате чего получится развертка верхней половины лепестка.