18. Плоскости частного положения.
Плоскость частного положения - плоскость проходящая через проецирующие прямые, т.е. перпендикулярная к одной или одновременно к двум основным плоскостям проекций. Если плоскость перпендикулярна только к одной плоскости проекций, то она называется проецирующей плоскостью.
Существует три вида проецирующих плоскостей:
Горизонтально-проецирующая плоскость - перпендикулярна к П1. И поэтому проецируется на нее как прямая.
Фронтально-проецирующая плоскость - перпендикулярна к П2. И поэтому проецируется на нее как прямая.
Профильно-проецирующая плоскость - перпендикулярна к П3. И поэтому проецируется на нее как прямая. На обычном ортогональном чертеже, когда плоскость П3 не используется, профильно-проецирующая плоскость выглядит как плоскость общего положения.
Если плоскость перпендикулярна к двум плоскостям проекций, то она называется плоскостью уровня. Следовательно, плоскость уровня всегда параллельна одной из плоскостей проекций. Существует три вида плоскостей уровня:
Горизонтальная плоскость уровня - || П1
Фронтальная плоскость уровня - || П2.
Профильная плоскость уровня - || П3.
19. Проведение перпендикуляра к плоскости.
П
ерпендикулярность
прямой и плоскости определяется основными
положениями: если одна сторона прямого
угла параллельна плоскости проекций,
то на эту плоскость прямой угол
проектируется без искажения; если прямая
перпендикулярна двум пересекающимся
прямым плоскости, она перпендикулярна
этой плоскости.
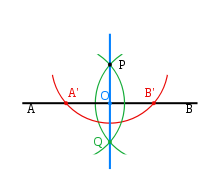
Построение перпендикуляра
Построение перпендикуляра:
Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А' и В'. Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A' и В' соответственно, проходящими через точку Р. Кроме точки Р есть ещё одна точка пересечения этих полуокружностей, назовём её Q. Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.
20. Построение линии пересечения плоскостей.
При решении задачи на построение линии пересечения двух плоскостей возможны два случая: - пересечение проецирующей плоскости с плоскостью общего положения; - пересечение двух плоскостей общего положения.
Линия пересечения двух плоскостей представляет собой множество точек, которые общие для данных плоскостей. Из этих точек выделяют опорные, с которых и начинается построение линии. К ним относят верхнюю и нижнюю точки относительно той либо иной плоскости, точки, находящиеся в зоне видимости, и другие важные для построения этой линии точки.
Для более точного построения искомой линии пересечения выбирается ряд вспомогательных поверхностей, находятся точки искомой линии пересечения, которые последовательно соединяются. Прежде чем выбрать вспомогательную поверхность, надо рассмотреть заданные поверхности и выявить на каждой из них каркасы графически простых линий (прямых, окружностей) и их положение относительно плоскостей проекций. Вспомогательные поверхности выбирают так, чтобы они пересекали заданные поверхности по простым линиям, проекции которых нетрудно построить. В качестве вспомогательных могут быть взяты плоскости частного и общего положения, сферы, реже применяются цилиндрические и конические поверхности. В зависимости от вида вспомогательных поверхностей существует несколько методов, из которых наибольшее применение получили метод секущих плоскостей и метод сфер. При построении линии пересечения особое внимание следует уделять опорным (характерным) точкам, расположенным на главных меридианах, экваторе, горле, ребрах, линиях обрыва исходных поверхностей, а также в секущей плоскости симметрии.
22. Виды проецирования.
-центральное |
-параллельное |
-косоугольное |
-прямоугольное |
Если проецирующие лучи исходят из одной точки, то проецирование называют центральным.
Центральную проекцию часто называют перспективой. Перспективу применяют при рисовании с натуры, в архитектуре, строительстве.
Если проецирующие лучи параллельны друг другу, то проецирование называется параллельным.
Частными случаями параллельного проецирования являются косоугольное и прямоугольное проецирования.
Косоугольное проецирование – это когда лучи параллельны и падают под острым углом к плоскости проекций.
Если проецирующие лучи перпендикулярны плоскости проецирования, то проецирование называется прямоугольным.
Применяют в науке, технике, производстве, так как они достаточно наглядны и выполнять их гораздо проще.