6. Метод прямоугольного треугольника.

Длину отрезка АВ можно определить из прямоугольного треугольника АВС |AС|=|A1B1|, |BС|=DZ , a-угол наклона отрезка к плоскости П1, b-угол наклона отрезка к плоскости П2. Для этого на эпюре из точки B1 под углом 900 проводим отрезок |B1B1* |=DZ, полученный в результате построений отрезок A1B1*и будет натуральной величиной отрезка АВ, а угол B1A1B1* =α. Рассмотренный метод называется методом прямоугольного треугольника.

Однако все построения можно объяснить, как вращение треугольника АВСвокруг стороны AС до тех пор, пока он не станет параллелен плоскости П1, в этом случае треугольник проецируется на плоскость проекций без искажения.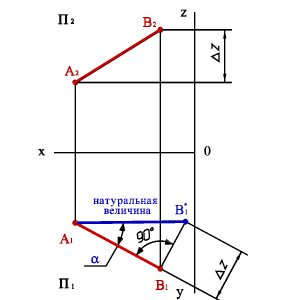

Cущность метода прямоугольного треугольника заключается в том, что:

натуральная величина прямой общего положения есть гипотенуза прямоугольного треугольника, одним из катетов которого является какая - либо проекция отрезка, а другим катетом служит разность расстояний концов другой проекции отрезка до оси чертежа, разделяющего эти отрезки.

7. Способы преобразования проекций.

Начертательная геометрия располагает способами, с помощью которых можно перейти от общих положений заданных геометрических образов к частным. Эти способы называются способами преобразования проекций, которые заключаются в последовательной замене плоскостей проекций и во вращении геометрических образов вокруг определенной оси.

Замена плоскостей проекций

Суть метода заключается в том, что одна из плоскостей проекций заменяется на новую плоскость проекций, при этом последнюю проводят перпендикулярно к незаменяе 949i84ej мой плоскости. При такой замене величина координаты любой точки на вводимой плоскости будет такой же, как координаты той же точки на заменяемой плоскости.

Вращение вокруг проецирующей оси

Этот метод заключается в том, что любая точка вращается вокруг какой-либо оси, перпендикулярной к одной из плоскостей проекции. При этом точка в пространстве движется по траектории окружности, которая лежит в плоскости, перпендикулярной к оси вращения. Система плоскостей проекций остается неизменной.

Метод плоскопараллельного перемещения

Суть метода заключается в том, что все точки фигуры перемещаются в пространстве параллельно некоторой плоскости (например, параллельно какой-либо плоскости проекций). Это означает, что каждая точка фигуры перемещается в соответствующей плоскости уровня.

Метод вращения вокруг линии уровня

Суть метода заключается в том, что осью вращения выбирается одна из линий уровня - горизонталь или фронталь плоскости или плоской фигуры. Таким образом, плоскость как бы поворачивается вокруг некоторой оси, принадлежащей этой плоскости, до положения, при которой эта плоскость становится параллельной одной из плоскостей проекций.

Метод совмещения плоскостей

Этот метод является частным случаем метода вращения вокруг линии уровня. В качестве оси вращения выбирается линия пересечения плоскости, в которой лежит та или иная фигура, с одной из плоскостей проекций. Иначе говоря, осью вращения служит горизонтальный или фронтальный след плоскости. При этом каждая точка, принадлежащая рассматриваемой фигуре, при вращении перемещается в плоскости, перпендикулярной к следу той плоскости, в которой она лежит.