Признак равномерной сходимости.

1) Признак Вейерштрасса (мажорантный признак)

П усть дан функциональный ряд 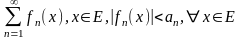и если – сходится, то функциональный ряд сходится равномерно на E.

Д оказательство (по критерию Коши):

Т.к. ряд сходится, то по критерию Коши: для

любого ε>0 существует такой номер N, что ε для всех n>N и любых целых p>=0. Поэтому для всех n>N и

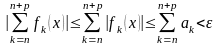. Это означает, что ряд

сходится равномерно на множестве Е

8. Интегрирование и дифференцирование функциональных рядов.

И нтегрирование и дифференцирование функциональных рядов.

Пусть имеется ряд (1)

Теорема о интегрировании и дифференцировании: Если ряд состоящий из непрерывных функций, сходится равномерно на [а, b] к сумме S(x), то интеграл от суммы этого ряда = сумме интегралов от его членов.

, где α и х є [a, b]

Д оказательство:

| |<ξ

По свойству определенного интеграла:

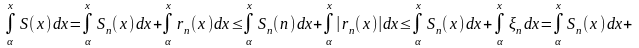
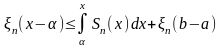
, т.к.

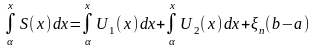
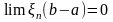
Дифференцирование функциональных рядов.

Теорема Если функциональный ряд (1) сходится к сумме S(x) на [a, b], и ряд (2) , составленный из производных членов данного ряда равномерно сходится на [a, b] к сумме σ(x), то сумма ряда, составленного из производных, равна производной от суммы ряда (1), т.е. σ(x)=

Доказательство: Т.к. 2-ой ряд сходится равномерно на [a, b], то по теореме интегрирования функциональных рядов.

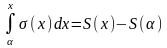
Продифференцируем по х:

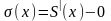
Что и требовалось доказать.

9. Степенные ряды. Теорема Абеля. Радиус сходимости. Вычисление радиуса

сходимости.

Степенным рядом называется функциональный ряд вида 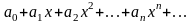, где 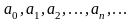- постоянные числа, называемые коэффициентами ряда.

Теорема Абеля.

Если степенной ряд сходится при некотором значении 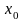, не равном нулю, то он абсолютно сходится при всяком х, для которого .

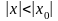Если ряд расходится при некотором значении , то он расходится при всяком х, для которого .

Доказательство: Так как по предположению числовой ряд 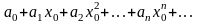сходится, то его общий член при , а это значит, что существует такое положительное число М, что все члены ряда по абсолютной величине меньше М. Перепишем ряд в виде и рассмотрим ряд из абсолютных величин его членов:

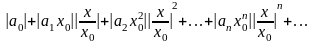Члены этого ряда меньше соответствующих членов ряда

При последний ряд представляет собой геометрическую прогрессию со знаменателем 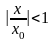и, следовательно, сходится.

Теперь нетрудно доказать и вторую часть теоремы: пусть в некоторой точке ряд расходится. Тогда он будет расходиться в любой точке х, удовлетворяющей условию . Действительно, если бы в какой-либо точке х-, удовлетворяющей этому условию, ряд сходился, то в силу только что доказанной первой части теоремы он должен был бы сходиться и в точке , так как 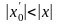. Но это противоречит условию, что в точке ряд расходится. Следовательно, ряд расходится и в точке х. Теорема полностью доказана.

Интервалом сходимости степенного ряда является такой интервал от –R до R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек х, лежащих вне его, ряд расходится. Число R называют радиусом сходимости степенного ряда.