1.)Числовые знако-ся ряды. Основные понятия. Ряд геометрической прогрессии.

Пусть дана число-ая последовательность {a_n }(от ∞ до n=1), тогда a₁ + a₂ + a₃ + …+ a_n … =

= ∑ (от ∞ до n=1) a_n наз-ся числовым рядом, если a_n ≥ 0 и n € N, то ряд наз-ся знакопол-ым.

Если среди элементов ряда некоторые a_k < 0, то ряд наз-ся знакоперем-ым.

n-ой частичной суммы ряда наз-ся выражение вида:

S_n = a + a₂ + a₃ + … + a_n = ∑ (от n до n=1) a_k , S₁ = a₁ , S₂ = a₁ + a₂ , S₃ = a₁ + a₂ + a₃

Если существует конечный предел последовательности n-ых частичных сумм ряда {S_n }(от ∞ до n=1), то ряд наз-ся сходящимся и его сумма равна числу S.

Lim (n-> ∞) S_n = S => ₁ + a₂ + a₃ + …+ a_n … = ∑ (от ∞ до n=1) a_n , ∑ (от ∞ до n=1) a_n = S

Ряд геометрической прогрессии:

b + bq + bq² +… bqⁿ + … = ∑ (от ∞ до n=0) bqⁿ , где b – 1-ый член, q – 2 член делим на 1-ый.

S_n = b(1-qⁿ)/1-q = b / 1-q – bqⁿ / 1-q , Lim (n-> ∞) S_n = (b / 1-q ) – b / 1-q Lim (n-> ∞) qⁿ

1. |q|<1 , Lim (n-> ∞) qⁿ = 0 => Lim (n-> ∞) S_n = b / 1-q = S , ∑ (от ∞ до n=0) bqⁿ = b / 1-q

2. |q|>1 , Lim (n-> ∞) qⁿ = ∞ (либо не существует), тогда ряд b + bq + bq² +… bqⁿ + … = ∑ (от ∞ до n=0) bqⁿ расходится и суммы не имеет.

3. |q|=1, b + b + b +… bⁿ + … = ∑ (от ∞ до n=0) bⁿ , Lim (n-> ∞) qⁿ = ∞ ряд расходится

4. q = -1 b - b + b –b+… ряд расходится, не существует Lim S_n.

Ряд геометрической прогрессии сходится, когда |q|<1 и расходится, если |q|≥1.

2.Необходимый признак сходимости числового ряда:

(1) a₁+а₂+а₃+…+а_n+…

Если числовой ряд (1) сходиться, то предел его n-го члена при n→∞ равен 0

Док-во: по определению ряд сходится =>

Сущ. lim_n→∞S_n=S

Если последовательность имеет предел, то он единственный

lim_n→∞S_n+1=S

lim_n→∞(S_n+1-S_n)=S-S=0

lim_n→∞a_n+1=0, ч.т.д.

Например(именно, что это необходимый признак):

1+1/2+1/3+1/4+…+1/n…

S_2n=1+1/2+1/3+…+1/n+1/(n+1)+…1/(2n)

S_n=1+1/2+1/3+…+1/n

S_2n-S_n=1/(n+1)+1/(n+2)+…+1/(2n) ≥n/(2n)=1/2

Если бы ряд сходился, то S_2n-S_n=0 => получили противоречие => ряд расходиться

Следствие: если lim_n→∞a_n≠0, то числовой ряд расходиться

Св-ва числовых рядов:

1) если ряд (1) сходиться в сумме S, то и ряд, полученный из данного при умножении a_i на λ (i=1,n), тоже сходиться, и его сумма равна λS.

Док-во: lim_n→∞S_n=S

S_n= a₁+a₂+a₃+…+a_n

δ_n= λa₁+ λa₂+ λa₃+…+ λa_n

lim_n→∞δ_n= λ lim_n→∞S_n= λS

2) Если сходиться ряд (1) в сумме S, и сходиться ряд (2) b₁+b₂+b₃+…+b_n в сумме δ, то и сходиться ряд 3 (a₁±b₁ +a₂±b₂ +a₃±b₃ +…+a_n±b_n+…) в сумме S±δ

Док-во: аналогично.

3. Достаточные признаки сходимости рядов с положительными членами (сравнения, Даламбера, Коши).

Признак сравнения.

Пусть имеем два ряда с положительными членами

a₁+a₂+…+a_n+…(1) и b₁+b₂+…+b_n+… (2), для которых выполняется условие: a_n b_n. Тогда 1) если сходится ряд (1), то сходится и ряд (2); 2) если ряд (2) расходится, то расходится и ряд (1) .

Док-во:

Поскольку 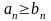и a_n, b_n — положительные, то м. утверждать: , где S_n и σ_n — n-частичные суммы 1-го и 2-го рядов;

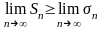
значит, если существует 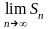(ряд 1 сходится), то существует и 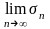(ряд 2 сходится)

Признак Даламбера.

Если в ряду с положительными членами отношение (n + 1)-го члена к n-му при 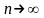имеет конечный предел l, то есть 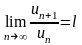, то

ряд сходится в случае ;

ряд расходится в случае ;

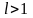3) в случае 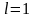ответа о сходимости или расходимости ряда теорема не дает.

Радикальный признак Коши.

Если для ряда с положительными членами величина имеет конечный предел l при , то есть , то

в случае ряд сходится;

в случае ряд расходится;

3) в случае ответа о сходимости или расходимости ряда теорема не дает.

Доказательство:

Пусть . Рассмотрим число q, удовлетворяющее соотношению 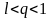. Начиная с некоторого номера n=N будет иметь место соотношение . Отсюда следует, что или для всех 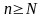. Рассмотрим теперь два ряда: 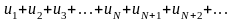(1) и (2). Ряд 2 сходится, так как его члены образуют убывающую геометрическую прогрессию. Члены ряда 1, начиная с 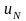, меньше членов ряда 2. Следовательно, ряд 1 сходится.

Пусть . Тогда, начиная с некоторого номера n=N будем иметь или 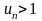. Но если все члены рассматриваемого ряда, начиная с , больше 1, то ряд расходится, так как его общий член не стремится к нулю.

Интегральный признак Коши.

Пусть члены ряда положительны и не возрастают, то есть 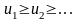и пусть f(х) – такая непрерывная не возрастающая функция, что , , .

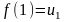Тогда справедливы следующие утверждения:

если несобственный интеграл 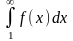сходится, то сходится и исходный ряд;

если указанный интеграл расходится, то расходится и исходный ряд.

Доказательство:

1) Предположим, что интеграл сходится, то есть имеет конечное значение. Так как 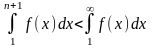, то , то есть частичная сумма Sn остается ограниченной при всех значениях n. Но при увеличении n она возрастает, так как все члены u_n положительны. Следовательно, Sn при имеет конечный придел 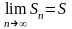, то есть ряд сходится.

2) Предположим далее, что 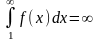. Это значит, что неограниченно возрастает при возрастании n. Но тогда Sn также неограниченно возрастает при возрастании n, то есть ряд расходится.

Обобщенный гармонический ряд.

Если члены знакопол-го ряда ∑ (от ∞ до n=1) a_n , могут быть представлены, как числовые значения,

некоторой непрерывной монотонно убывающей на промежутке [1;+∞] функции f(x) так, что

а₁=f(1) , а₂=f(2), … а_n=f(n), … то:

1. Если ∫ (от + ∞ до 1) f(x)dx сходя, то сходя ряд a₁ + a₂ + a₃ + …+ a_n … = ∑ (от ∞ до n=1) a_n

2. Если ∫ (от + ∞ до 1) f(x)dx расход, то расход ряд a₁ + a₂ + a₃ + …+ a_n … = ∑ (от ∞ до n=1) a_n