
- •1. Двумерная система координат
- •2. Трехмерная и n-мерная система координат
- •3. Ориентация осей
- •Общее уравнение прямой
- •Параметрические уравнения прямой
- •Каноническое уравнение прямой
- •3. Уравнения пучка прямых, проходящих через заданную точку.
- •Нормальное уравнение прямой. Расстояние от данной точки до данной прямой
Билет 1)Понятие матрицы, виды матриц. Линейные операции над матрицами
Ответ:
Матрицей N*Mназывается прямоугольная
таблица изMстрок и Nстолбцов, состоящая
из чисел или иных математических
выражений. Виды матриц: Квадратная,
Диагональная, Единичная, Нулевая.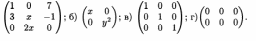

Билет 2)Умножение матриц. Важнейшие свойства умножения матриц.




Билет 3)Понятие детерминанта (определителя) матрицы, индуктивное определение. Элементарные преобразования матриц. Изменение детерминанта в результате элементарных преобразований матрицы.
Определитель,
или детерминант —
одна из важнейших характеристик
квадратных матриц. Определитель матрицы
размераn
× n равен
ориентированному n-мерному объёму
параллелепипеда, натянутого на её
векторы-строки (или столбцы).
Для
матрицы n
× n определитель
выражается в виде многочлена степени
N от элементов матрицы который представляет
собой сумму произведений элементов
матрицы со всевозможными комбинациями
различающихся номеров строк и столбцов,
причём в каждом из произведений элемент
из любой строки и любого столбца ровно
один. Каждому произведению приписывается
знак плюс или минус в зависимости от
чётности перестановки номеров.
Если
элементами матрицы являются числа, то
определитель — это тоже число. В общем
случае определитель может быть
функциональным, векторным и т.п., то
есть, представлять собой иные выражения,
составленные из элементов.

Алгоритмы решения целого ряда задач включают в себя (в качестве составных элементов) элементарные преобразования матриц, к числу которых относятся:
умножение строки или столбца матрицы на ненулевое число; перестановка местами двух строк или столбцов матрицы; прибавление к некоторой строке матрицы другой ее строки, предварительно умноженной на произвольный коэффициент; прибавление к некоторому столбцу матрицы другого ее столбца, предварительно умноженного на произвольный коэффициент.

Билет4)Линейная зависимость и линейная независимость между строками (столбцами) матицы. Критерий равенства нулю определителя квадратной матрицы. Понятия линейной зависимости и линейной независимости определяются для строк и столбцов одинаково. Поэтому свойства, связанные с этими понятиями, сформулированные для столбцов, разумеется, справедливы и для строк.
1. Если в систему столбцов входит нулевой столбец, то она линейно зависима.
2. Если в системе столбцов имеется два равных столбца, то она линейно зависима.
3. Если
в системе столбцов имеется два
пропорциональных столбца 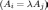 ,
то она линейно зависима.
,
то она линейно зависима.
4. Система
из  столбцов
линейно зависима тогда и только тогда,
когда хотя бы один из столбцов есть
линейная комбинация остальных.
столбцов
линейно зависима тогда и только тогда,
когда хотя бы один из столбцов есть
линейная комбинация остальных.
5. Любые столбцы, входящие в линейно независимую систему, образуют линейно независимую подсистему.
6. Система столбцов, содержащая линейно зависимую подсистему, линейно зависима.
7. Если
система столбцов 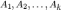 —
линейно независима, а после присоединения
к ней столбца
—
линейно независима, а после присоединения
к ней столбца  —
оказывается линейно зависимой, то
столбец
можно
разложить по столбцам
,
и притом единственным образом, т.е.
коэффициенты разложения находятся
однозначно.
—
оказывается линейно зависимой, то
столбец
можно
разложить по столбцам
,
и притом единственным образом, т.е.
коэффициенты разложения находятся
однозначно.
Критерии равенства нулю определителя: 1) Если у определителя какая-либо строка(столбец) состоит только из нулей, то определитель равен 0.2) Если какие-то две строки(два столбца) определителя пропорциональны, то определитель равен 0.
Билет 5)Понятие матрицы, обратной к данной. Критерий существования обратной матрицы. Алгебраическое дополнение к данному элементу квадратной матрицы. Союзная матрица. Нахождение обратной матрицы с использованием союзной матрицы.

Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица
А = (А1, А2,...Аn)
называется невырожденной,
если векторы-столбцы являются линейно
независимыми. Число линейно независимых
векторов-столбцов матрицы называется
рангом матрицы  .
Поэтому можно сказать, что для того,
чтобы существовала обратная матрица,
необходимо и достаточно, чтобы ранг
матрицы равнялся ее размерности, т.е. r
= n.
.
Поэтому можно сказать, что для того,
чтобы существовала обратная матрица,
необходимо и достаточно, чтобы ранг
матрицы равнялся ее размерности, т.е. r
= n.
(союзная, взаимная, присоединённая) матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы. Из определения следует, что присоединённая матрица рассматривается только для квадратных матриц и сама является квадратной, ибо понятие алгебраического дополнения вводится для квадратных матриц.
Билет 6)Понятие ранга системы строк, ранга системы столбцов матрица. Ранг матрицы. Теорема о ранге матрицы.
Рангом матрицы A по строкам называется размерность подпространства, порожденного векторами-строками этой матрицы, а рангом матрицы A по столбцам — размерность подпространства, порожденного векторами-столбцами этой матрицы. Ранг матрицы A по строкам обозначается через rs (A), а ранг A по столбцам — через rc (A). Рангом матрицы по минорам называется наибольший из порядков тех миноров этой матрицы, которые не равны нулю. Ранг матрицы A по минорам обозначается через rm(A)

Теорема. Элементарные преобразования не изменяют ранг матрицы.
Для доказательства теоремы достаточно убедиться в том, что в результате элементарных преобразований нулевой определитель остается нулевым, а ненулевой – ненулевым.
Перестановка строк или столбцов матрицы изменяет только знак определителя.
При умножении строки (столбца) матрицы на ненулевое число определитель умножается на это число.
Определитель не изменяется, если к строке (столбцу) прибавляется другая строка (столбец).
Таким образом, в результате элементарных преобразований сингулярные матрицы остаются сингулярными, а несингулярные – несингулярными.
Билет7)Теорема о базисном миноре. Описание процедуры нахождения базисного минора методом окаймления.


Метод
окаймляющих миноров нахождения ранга
матрицы А состоит в следующем.

Билет 8)Системы линейных алгебраических уравнений. Виды систем: совместные и несовместные, определенные и неопределенные, однородные и неоднородные.

Если все свободные члены системы линейных уравнений равны 0, то система называется однородной, в противном случае — неоднородной. Если в системе (2) все свободные члены заменить нулями, то мы получим однородную систему
Билет 9)Критерий разрешимости системы линейных уравнений (Теорема Кронекера-Капелли), идея доказательства. Критерий определенности системы линейных алгебраических уравнений.
Матрица,
получающаяся конкатенацией матрицы  и
столбца правых частей
и
столбца правых частей 
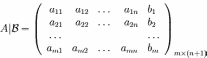
называется расширенной матрицей системы линейных уравнений.
Теорема [Кронекер, Капелли]. Система совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:
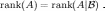
При
выполнении этого условия, система имеет
единственное решение, если число
неизвестных  совпадает
с общим значением ранга
совпадает
с общим значением ранга  , и
бесконечное множество решений,
если
меньше
этого значения.
, и
бесконечное множество решений,
если
меньше
этого значения.
Доказательство необходимости.
Пусть существует решение 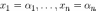 системы,
тогда
системы,
тогда

т.е.
столбец  линейно
выражается через столбцы
линейно
выражается через столбцы 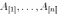 .
Но тогда
.
Но тогда
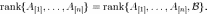
Следовательно 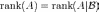 .
.
Билет 10)Решение системы линейных уравнений по правилу Крамера. Условия применимости правила Крамера и его связь с решением системы с помощью обратной матрицы

Условия: Если D – определитель матрицы А- не равно нулю, то система совместна и определена, ее решение задается формулой : Х=А (в степени -1) умножить на В.
Билет 11)Метод Гаусса решения систем линейных алгебраический уравнений. Нахождение матрицы обратной данной методом Гаусса.

Билет 12)Теорема об общем виде общего решения системы линейных алгебраических уравнений. Описание процедуры нахождения общего решения системы линейных уравнений.
http://www.cleverstudents.ru/solving_systems_of_linear_equations.html
http://www.exponenta.ru/EDUCAT/CLASS/courses/la/theme4/theory.asp
Билет 13 Понятие геометрического вектора. Линейные операции над векторами. (страница 91)

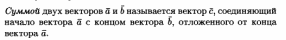

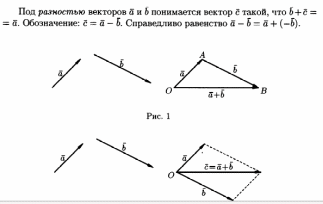
Билет14)Понятие базиса векторного пространства. Координатная форма вектора. Линейные операции над векторами в координатной форме.
Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве. Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.

Билет 15)Понятие скалярного произведения, его свойства (линейность по каждому сомножителю, коммутативность, геометрическая интерпретация).
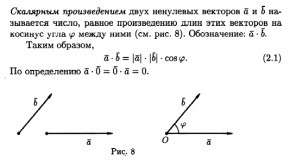

Билет 16)Скалярное произведение векторов, заданных в координатной форме. Частный вид скалярного произведения векторов Заданных в ортонормированном базисе.
Понятие скалярного произведения
Скалярное произведение — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.
Обычно используется одно из следующих обозначений:
 ,
,
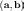 ,
,
 ,
,
или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):
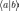 .
.
Обычно предполагается, что скалярное произведение положительно определено, то есть
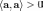 для
всех
для
всех 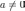 .
.
Если этого не предполагать, то произведение называется индефинитным.
Скалярным
произведением векторов  и
и  называется
произведение их длин на косинус угла
между ними:
называется
произведение их длин на косинус угла
между ними:
|
Совершенно аналогично, как в планиметрии, доказываются следующие утверждения:
Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Скалярный квадрат вектора, то есть скалярное произведение его самого на себя, равно квадрату его длины.
Скалярное произведение двух векторов
 и
и 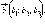 заданных
своими координатами, может быть вычислено
по формуле
заданных
своими координатами, может быть вычислено
по формуле 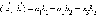
Векторное произведение векторов в ортонормированном базисе

Билет 17)Понятие ориентации тройки геометрических векторов. Правый и левый ортонормированный базис.
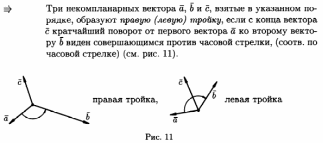
Билет18)Понятие векторного произведения, его свойства: антикоммута-тивность, линейность по каждому сомножителю. Критерий кол-линеарности двух векторов.


Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору.
Таким
образом, мы пришли к необходимому
и достаточному условию коллинеарности
двух ненулевых векторов:
для коллинеарности двух
векторов 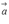 и
и 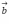 необходимо
и достаточно, чтобы они были связаны
равенствами
необходимо
и достаточно, чтобы они были связаны
равенствами  или
или  .
.
Билет19)Векторное произведение векторов, заданных в ортонормированном базисе

Билет 20)Понятие смешанного произведения трех векторов, его геометрическая интерпретация. Линейность смешанного произведения по каждому сомножителю.


Линейность операции по какому-то аргументу означает выполнение двух условий:
1) если аргумент умножить на число, то и результат умножится на это число, то есть числовой множитель аргумента можно вынести за знак операции;
2) если аргумент заменить суммой двух слагаемых, то результат будет равен сумме результатов для каждого слагаемого.
Билет 21)Вид смешанного произведения векторов, заданных в ортонормированном базисе.


Билет 22)Введение координат в двумерной и трёхмерной геометрии. Уравнение прямой в (планиметрия) в каноническом виде, параметрическом и общем виде .
Декартову систему координат (или прямоугольная система координат) впервые предложил известный французский математик Рене Декарт около 1637 г.
1. Двумерная система координат
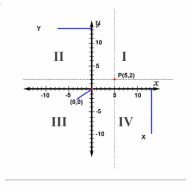
Точка P имеет координаты (5,2).
Современная Декартова система координат в двух измерениях (также известная под названием прямоугольная система координат) задается двумя осями, расположенными под прямым углом друг к другу. Плоскость, в которой находятся оси, называют иногда xy-плоскости. Горизонтальная ось обозначается как x(ось абсцисс), вертикальная как y (ось ординат).
Все точки в системе декартовых координат, составляют так называемое Декартово пространство.
Точка пересечения, где оси встречаются, называется началом координат и обозначается как O. Соответственно, ось x может быть обозначена как Ox, а ось y - как Oy.
Прямые, проведенные параллельно каждой оси на расстоянии единичного отрезка (единицы измерения длины) начиная с начала координат, формируют координатную сетку. Таким образом, координаты формируют упорядоченную пару (кортеж) чисел (x, y).В трехмерном пространстве добавляется еще z-координата (расстояние точки от ху-плоскости), и формируется упорядоченная тройка координат (x, y, z).
Стрелки на осях отражают то, что они простираются до бесконечности в этом направлении.
Пересечение двух осей создает четыре квадранта на координатной плоскости, которые обозначаются римскими цифрами I, II, III, и IV. Обычно порядок нумерации квадрантов - против часовой стрелки, начиная с правого верхнего (т.е. там, где абсциссы и ординаты - положительные числа). Значение, которых приобретают абсциссы и ординаты в каждом квадранте, можно свести в следующую таблицу:
Квадрант |
x |
y |
I |
> 0 |
> 0 |
II |
<0 |
> 0 |
III |
<0 |
<0 |
IV |
> 0 |
<0 |
|
|
|
2. Трехмерная и n-мерная система координат

На этом рисунке точка P имеет координаты (5,0,2), а точка Q - координаты (-5, -5,10)
Координаты в трехмерном пространстве формируют тройку (x, y, z)
Координаты x, y, z для трехмерной декартовой системы можно понимать как расстояния от точки до соответствующих плоскостей: yz, xz, и xy.
Трехмерная Декартова система координат является очень популярной, так как соответствует привычным представлениям о пространственных измерения - высоту, ширину и длину (то есть три измерения). Но в зависимости от области применения и особенностей матиматичного аппарата, смысл этих трех осей может быть совсем другим.
3. Ориентация осей
В трехмерных декартовых координатах является неоднозначность: как только направления осей x и у выбран, ось z может быть направлена как в одну сторону от xy-плоскости, так и в другую. Это требует специального определения понятия ориентации системы координат. Для трехмерной системы эти две возможности ориентации осей принято называть "левой" и "правой". Системы координат при этом называют "левой" и "правой" соответственно. Они изображены на следующем рисунке:

Левая ориентация - слева, правая ориентация - справа.
Общепринятой считается "права" ориентация, хотя левая тоже применяется.

