
- •Раздел 1. Накопление и обработка данных .…………………………… 5
- •Раздел 2. Оперативный анализ данных ….…………………………… 43
- •Раздел 3. Интеллектуальный анализ данных ………………………… 82
- •Раздел 4 Загрузка данных и программирование запросов ...………… 110
- •Раздел 5. Подготовка отчетов по результатам анализа …….……… 136
- •Раздел 1. Накопление и обработка данных Лекция 1. Информационно-аналитические системы
- •Операционная обработка данных
- •Оперативный анализ данных
- •Интеллектуальный анализ данных
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Лекция 2. Концепции хранения данных
- •Реляционные базы данных
- •Организация хранилищ данных
- •Концепция многомерной модели данных
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Лекция 3. Интеграция и трансформации данных
- •Платформа sql Server 2008
- •Система Management Studio
- •Служба sql Server Integration Services
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Раздел 3. Интеллектуальный анализ данных Лекция 8. Кластерный анализ данных
- •Формальная постановка задачи кластеризации
- •Меры близости в кластерном анализе
- •Иерархические алгоритмы кластеризации
- •Неиерархические алгоритмы кластеризации
- •Представление результатов кластеризации
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Лекция 9. Классификация и регрессия
- •Математические функции
- •Правила классификации
- •Деревья решений
- •Методы построения деревьев решений
- •Алгоритмы построения деревьев решений
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Лекция 10. Поиск ассоциативных правил
- •Цель лекции – изучение формализованной постановки и алгоритма решения задачи поиска ассоциативных правил.
- •Формальная постановка задачи
- •Обнаружение закономерностей в последовательностях данных
- •Алгоритм поиска ассоциативных правил Apriori
- •Представление результатов
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Лекция 8. Службы sql Server Analysis Services
- •Конструктор интеллектуального анализа данных
- •Мастер интеллектуального анализа данных
- •Создание структуры интеллектуального анализа
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Создание и представление источника данных
- •Загрузка с применением Integration Services
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Лекция 12. Основы языка Multidimensional Expressions
- •Оператор select
- •Алгебра множеств и операции с множествами
- •Функции языка mdx
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Лекция 13. Язык операций Data Mining
- •Ключевые концепции и объекты dmx
- •Синтаксис запросов dmx
- •Создание моделей интеллектуального анализа
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Раздел 5. Подготовка отчёта по итогам анализа Лекция 14. Служба отчетов Reporting Services
- •Архитектура службы отчётов
- •Средства проектирования запросов
- •Развёртывание Reporting Services
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Лекция 15. Источники данных для отчётов
- •Общие источники данных
- •Источники поддерживаемые Reporting Services
- •Создание, изменение и удаление источников
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Лекция 16. Конструирование и создание отчётов
- •Основы конструирования отчётов
- •Создание нерегламентированных отчётов
- •Создание отчётов с применением конструктора
- •Краткие итоги
- •Контрольные вопросы
- •Литература
- •Глоссарий
Формальная постановка задачи кластеризации
Формальная постановка
задачи кластеризации осуществляется
следующим образом. Определяется множество
объектов данных
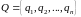 .
Каждый объект
.
Каждый объект
 характеризуется набором атрибутов:
характеризуется набором атрибутов:
 .
.
Примером такого множества объектов может быть коллектив преподавателей высшего учебного заведения, каждый из которых характеризуется набором показателей (атрибутов) о квалификации, учебно-методической и научной деятельности, внеаудиторной работе.
Каждая переменная
из набора
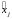 принимает значения из множества
действительных чисел
принимает значения из множества
действительных чисел
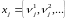 .
Решением задачи кластеризации является
множество сформированных кластеров
.
Решением задачи кластеризации является
множество сформированных кластеров
 ,
,
где
 -
кластер, содержащий
похожие объекты из множества
-
кластер, содержащий
похожие объекты из множества
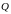 ,
,
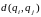 -
мера близости между объектами,
-
мера близости между объектами,
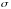 -
величина, определяющая меру близости
между объектами.
-
величина, определяющая меру близости
между объектами.
Мера близости должна отвечать следующим условиям [1, 2]:
а)
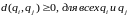 ;
;
б)
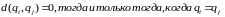 ;
;
в)
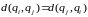 ;
;
г)
 .
.
При выполнении
неравенства
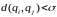 объекты из множества
рассматриваются как близкие и помещаются
в один кластер. Иначе объекты помещаются
в разные кластеры.
объекты из множества
рассматриваются как близкие и помещаются
в один кластер. Иначе объекты помещаются
в разные кластеры.
Меры близости в кластерном анализе
В задачах кластеризации
выбор меры близости предполагает
представление объектов в виде точек
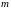 -
мерного пространства
-
мерного пространства
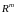 .
При этом меры близости определяют
расстояние между двумя точками
пространства
.
Наибольшее применение находят следующие
меры: евклидово
расстояние, расстояние по Хеммингу,
расстояние Чебышева, расстояние
Махаланобиса.
.
При этом меры близости определяют
расстояние между двумя точками
пространства
.
Наибольшее применение находят следующие
меры: евклидово
расстояние, расстояние по Хеммингу,
расстояние Чебышева, расстояние
Махаланобиса.
Евклидово расстояние между объектами вычисляется по формуле:
 .
.
Данная мера придаёт большие веса более отдалённым друг от друга объектам из заданного множества .
Расстояние по Хеммингу вычисляется следующим образом:
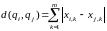 .
.
Эта мера в отличие от расстояния Евклида снижает влияние больших разностей по отдельным атрибутам на результаты кластеризации.
Для оценки расстояния по Чебышеву используется формула:
 .
.
Как правило, формула Чебышева используется при необходимости разнести объекты по кластерам, имеющим существенное различие только по одному атрибуту (измерению).
Расстояние Махаланобиса вычисляется по формуле:
 ,
,
где – ковариационная
матрица размерности
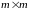 ,
,
 - символ транспонирования [1].
- символ транспонирования [1].
К настоящему времени известно более 100 алгоритмов кластерного анализа. Все алгоритмы разделяют на иерархические и неиерархические алгоритмы.
Иерархические алгоритмы кластеризации
Иерархические алгоритмы кластерного анализа в свою очередь разделяют на агломеративные и дивизимные.
В иерархических
агломеративных алгоритмах кластеризации
исходное множество объектов
представляется как множество кластеров
 .
Таким образом, на первом шаге алгоритма
имеем:
.
Таким образом, на первом шаге алгоритма
имеем:
 и
и
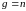 .
.
На втором
шаге алгоритма, используя выбранную
меру близости
 ,
находят кластеры с наименьшим удалением
друг от друга и осуществляют слияние
кластеров
,
находят кластеры с наименьшим удалением
друг от друга и осуществляют слияние
кластеров
 в общий кластер
в общий кластер
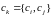 .
Процесс поиска кластеров с наименьшим
удалением и их слияние повторяют. В
результате формируются множества
кластеров мощностью
.
Процесс поиска кластеров с наименьшим
удалением и их слияние повторяют. В
результате формируются множества
кластеров мощностью
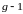 ,
,
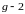 ,
,
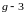 ,
…. Пересчет расстояния между кластером
,
…. Пересчет расстояния между кластером
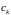 и кластером
и кластером
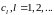 выполняют по формуле:
выполняют по формуле:
 ,
,
где
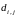 –
расстояние между кластерами
–
расстояние между кластерами
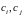 ,
,
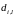 –
расстояние между кластерами
–
расстояние между кластерами
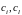 ,
,
 –
расстояние между кластерами
–
расстояние между кластерами
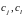 ,
,
 –
весовые коэффициенты. В методе медиан
используются следующие значения
коэффициентов:
–
весовые коэффициенты. В методе медиан
используются следующие значения
коэффициентов:
 [1].
[1].
В дивизимных алгоритмах исходное множество представляется как единственный кластер. Таким образом, на первом шаге имеем:
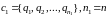 .
.
На втором
шаге алгоритма выбирается объект
 ,
который наиболее удален от других
объектов в этом кластере. Удаление
объекта
определяется как наибольшее среднее
расстояния до других объектов кластера
и рассчитывается по формуле:
,
который наиболее удален от других
объектов в этом кластере. Удаление
объекта
определяется как наибольшее среднее
расстояния до других объектов кластера
и рассчитывается по формуле:
 .
.
Формируется
новый кластер
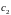 .
Выбранный объект
удаляется из кластера
.
Выбранный объект
удаляется из кластера
 и помещается в кластер
(
и помещается в кластер
( ).
На последующих шагах алгоритма объекты
из кластера
,
у которых разность значений между
средним расстоянием до объектов в
и средним расстоянием до объектов в
наибольшая, переносятся в
.
Перенос объектов из
в
продолжается до тех пор, пока разности
средних расстояний не станут отрицательными.
В результате выполнения последовательности
шагов формируются два кластера.
).
На последующих шагах алгоритма объекты
из кластера
,
у которых разность значений между
средним расстоянием до объектов в
и средним расстоянием до объектов в
наибольшая, переносятся в
.
Перенос объектов из
в
продолжается до тех пор, пока разности
средних расстояний не станут отрицательными.
В результате выполнения последовательности
шагов формируются два кластера.
К одному из сформированных кластеров применяют рассмотренную выше процедуру разделения. Выбор кластера для разделения может осуществляться на основе оценки диаметров кластеров. Оценка диаметра кластеров выполняется с применением формулы:
 ,
,
 .
.
Разделение кластеров производится до тех пор, пока все члены одного кластера не будут отвечать требованию близости или все кластеры будут содержать по одному объекту.
