25. Поток Эрланга первого, второго и третьего порядка.

Пусть имеется поток вызовов, для которого t₁, t₂,... есть моменты поступления вызовов. Выберем из этого потока часть вызовов, применив следующую операцию: вызов, поступающий в момент t_k (k=1, 2, ...), с вероятностью ρ остается в новом потоке и с вероятностью (1.ρ) теряется. Новый поток вызовов называется просеянным. Таким образом, просеянный поток образуется из заданного потока, в котором случайное число вызовов теряется, следующий вызов остается (просеивается), затем снова случайное число вызовов, имеющее тот же закон распределения, теряется, следующий вызов заданного потока остается и т. д. Операция, с помощью которой получен просеянный поток, называется рекуррентной операцией просеивания. Поток, получаемый из рекуррентного потока с помощью рекуррентной операции просеивания, также является рекуррентным.

Если основной поток . простейший с параметром λ и каждый вызов этого потока просеивается с вероятностью р и теряется с вероятностью (1.ρ), то просеянный поток будет также простейшим с параметром λρ. Из этого следует весьма важный для практики вывод: если поступающий на коммутационную систему простейший поток с параметром λ разделяется на h направлений и вероятность того, что вызов входящего потока поступает на i-е направление (i=1,2, ..., h), равна ρ_i, то поток i-го направления является также простейшим с параметром λρ_i.

Используем отличную от рекуррентной операцию просеивания, при которой точно m вызовов потока теряются, (m+1)-й вызов просеивается, затем снова точно m вызовов теряются и (m+1)-й просеивается и т. д. В результате такой операции просеивания простейшего потока образуется так называемый поток Эрланга m-го порядка. Если в простейшем потоке сохранить (просеять) каждый третий вызов, то образуется поток Эрланга 2-го порядка, каждый второй вызов . поток Эрланга 1-го порядка. Естественно, простейший поток можно рассматривать как поток Эрланга нулевого порядка.

В потоках Эрланга любого порядка промежутки времени между вызовами независимы и распределены по одному и тому же закону, так как эти промежутки представляют собой сумму одинакового числа промежутков простейшего потока. В связи с этим потоки Эрланга являются рекуррентными.

Математическое ожидание M(Z_m), дисперсия D(Z_m) и среднеквадратическое отклонение σ(Z_m) промежутка времени между вызовами в потоке Эрланга m-го порядка равны соответственно

Из (2.36) и (2.37) следует, что с увеличением порядка потока Эрланга увеличиваются математическое ожидание и дисперсия промежутка времени между вызовами и одновременно уменьшается параметр потока. Потоки Эрланга m-го порядка при разных т создают потоки с различной степенью случайности: от простейшего (m = 0) до детерминированного (m = ∞).

26. Примеры простейших самоподобных процессов.

Простым примером самоподобных случайных последовательностей может служить случайное движение точки, начиная с некоторого момента времени , когда она находилась в нуле. В каждые последующие моменты времени  ее координата меняется на произвольную случайную добавку . Тогда модель движения можно описать как

, т.е. текущая координата определяется на основе предыдущей плюс случайное смещение. Если СВ  подчиняется нормальному закону распределения

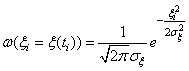с нулевым математическим ожиданием и дисперсией , то формируемый процесс  будет представлять собой броуновское движение частицы (стохастический винеровский процесс).

Рассмотрим координату частицы  в момент времени . Величина  будет состоять из случайных добавок  в предшествующие моменты времени, т.е.

.

Следовательно, математическое ожидание координаты частицы

,

а дисперсия .

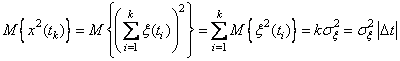Таким образом, при  математическое ожидание СВ  равно нулю, а дисперсия стремится к бесконечности. Кроме того, для любых двух моментов времени  и , дисперсия разности .

Так как процесс  представляет собой суммы гауссовских случайных величин и известную дисперсию для каждого момента времени , то можно записать ПРВ данной величины в виде

, где  - координата или приращение координаты броуновской частицы (т.к. данный процесс в момент времени  равен нулю);  - интервал времени наблюдения.

Для того чтобы процесс  обладал свойством самоподобности, т.е. являлся фракталом, достаточно значение дисперсии  заменить на , где  - параметр Херста. Такая замена приводит к тому, что отсчеты стохастического броуновского движения становятся коррелированными между собой, т.е. . Следовательно, можно записать, что

.

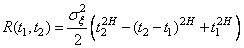Корреляция приращений  и  может быть определена как

В дискретном случае, когда величины  и  заменяются на  и  соответственно, получаем следующую корреляционную функцию для приращений фрактального броуновского движения

.

Последовательность случайных приращений с данной корреляционной функцией называется фрактальным гауссовским шумом. Причем коэффициент корреляции , при  и определяет долговременную зависимость между отсчетами случайного процесса. Корреляционная функция  отличается от гауссовских  и экспоненциальных  тем, что предполагает спад в корреляции при увеличении  заметно более медленный, что согласуется с результатами наблюдений интенсивностей в реальных трафиках с пакетной коммутацией. Кроме того, она полностью описывается только двумя параметрами – дисперсией и показателем .