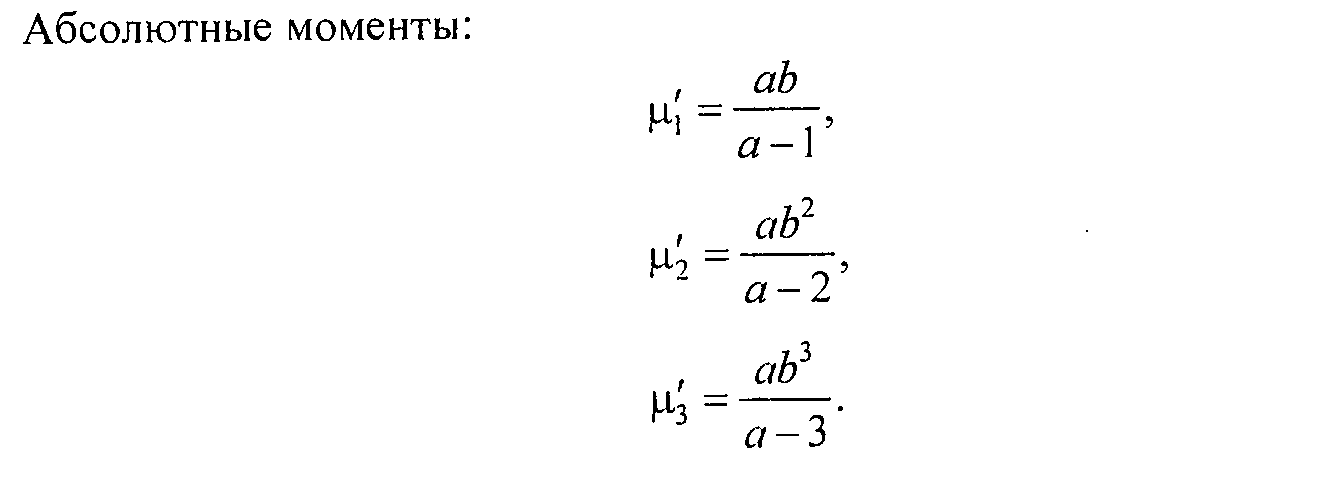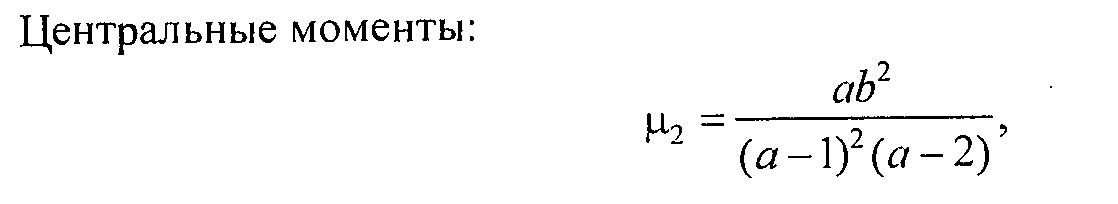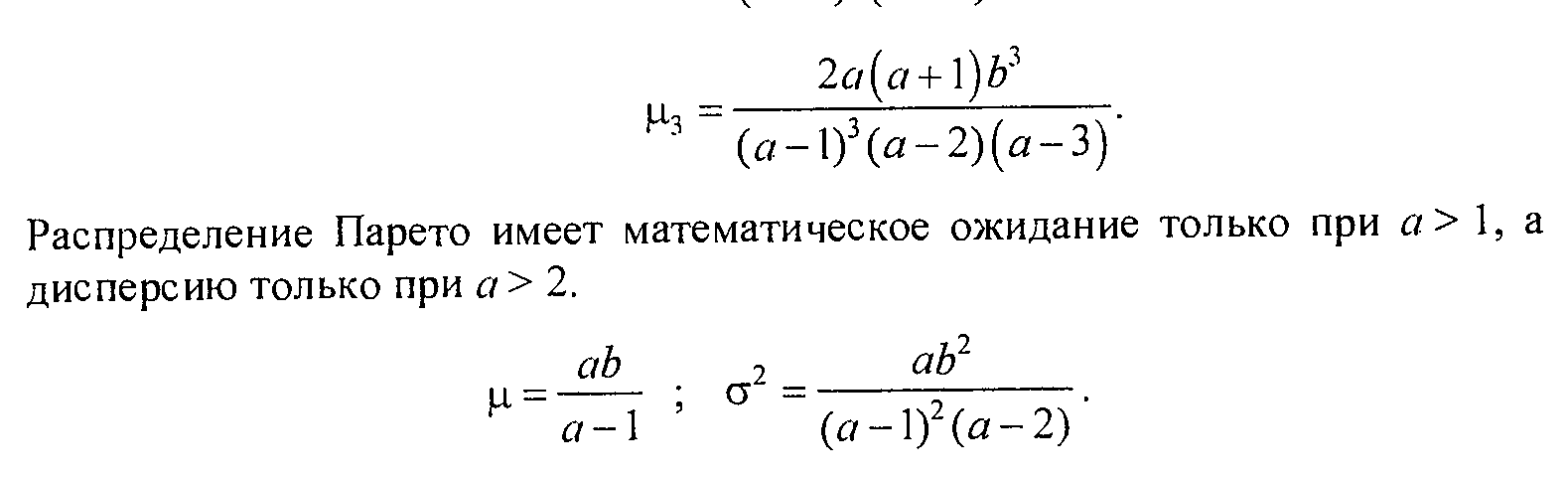- •Определение средней интенсивности трафика. Единица измерения интенсивности трафика.
- •Измерения трафика. Диаграмма Ганта. Нахождение объема пропущенного трафика. Средняя интенсивность трафика.
- •Нормальная оценка интенсивности трафика.
- •4. Диаграмма Кивиата для телефонной линии.
- •5. Как определяется объем трафика и интенсивность трафика?
- •2) Пусть в течение времени т фиксируются длительности ti всех n занятий выходов некоторого пучка, тогда трафик определяют так:
- •6. Программы для мониторинга сетей. Функции и возможности.
- •7. Основные понятия модели потоков событий ( стационарность, последействие, ординарность, интенсивность потока, параметр потока).
- •8 Что такое пуассоновский поток? Перечислите его свойства, параметры.
- •9 Определение примитивного потока
- •20 Примеры самоподобных процессов.
- •21. Основные принципы моделирования потока событий.
- •23. Распределение Вейбулла: математическое ожидание, дисперсия, абсолютные моменты, центральные моменты.
- •24. Самоподобные (фрактальные) модели трафика.
- •25. Поток Эрланга первого, второго и третьего порядка.
- •26. Примеры простейших самоподобных процессов.
- •27. Понятие фрактала. Основное свойство фракталов. Виды фракталов.
- •28. Нормированное фрактальное броуновское движение с параметром Херста.
- •29. Фрактальный гауссовский шум.
- •30. Генерирование потока событий с равномерным распределением интервала между событиями.
- •31. Генерирование потока событий, распределенных по закону, отличному от равномерного.
- •32. Модели потоков событий. Метод удачного случайного приращения.
- •33. Модели потоков событий. Метод случайного смещения промежуточных точек
- •34. Модели систем массового обслуживания.
- •35. Задачи анализа и проектирования телекоммуникационных сетей и систем
- •36. Понятие масштабной модели, её назначение и возможности. Анализ недостатков данной модели
- •37. Физическая модель сети типа прототип, её назначение и возможности. Анализ недостатков данной сети.
- •41. Формула Литла для определения среднего числа заявок в системе.
- •45. Смо с полнодоступными и неполнодоступными серверами.
- •47. Анализ механизма приоритетного обслуживания (в лекциях тема 7).
- •46. Анализ работы смо без приоритетов.
- •48. Виды различных дисциплин обслуживания требований.
- •49. Определение среднего времени ожидания в очереди для меченного требования
- •50. Определение консервативной смо. Формула для определения взвешенной суммы времени ожидания в очереди
- •51. Имитационные модели смо, основные задачи построения программы имитации
- •52. Условия, накладываемые на быстродействие алгоритмов имитации
- •68. Непрерывные цепи Маркова.
- •69.Анализ системы «гибели-размножения». Графическая интерпретация процессов переходов в непрерывной цепи Маркова.
- •70. Диаграмма интенсивностей переходов для непрерывной цепи Маркова.
- •71.Уравнения равновесия или баланса.
- •72. Анализ системы массового обслуживания типа m/m/1, диаграмма интенсивностей переходов в этой системе.
- •73 Стационарное распределение вероятностей состояний в системе m/m/1, зависимость среднего времени пребывания в системе в зависимости от коэффициента использования (нагрузки).
- •75. Сравнение характеристик качества обслуживания двухсерверной системы с односерверной.
- •81. Анализ характеристик качества обслуживания системы.
- •85.Модель Энгсета. Схема m-серверной системы с полными потерями
- •86. Диаграмма интенсивностей переходов для m-серверной системы с полными потерями, соответствующей модели Энгсета
- •90 Система с самоподобным входным потоком и детерминированным временем обслуживания
- •91 Расчет основных характеристик системы с самоподобным входным потоком и детерминированным временем обслуживания.
- •92 Анализ телекоммуникационных систем.
- •93. Расчет необходимого числа соединительных линий.
- •95. Анализ сетей массового обслуживания.
- •96 Марковские сети без потерь
- •97 Пример замкнутой сети с тремя узлами. Диаграмма переходов для этой сети.
- •98 Сети с блокировками (потерями). Метод Ли.
- •99. Сравнительный анализ расчетов соединительных линий
- •100 Анализ многозвеньевых коммутационных схем
20 Примеры самоподобных процессов.
Представленный пример фрактала (кривая Коха) относится к классу детерминированных фракталов, т. е. когда объект непосредственно составляется из своих малых копий. В теории телетрафика для описания поведения величины нагрузки в сетях связи с пакетной коммутацией применяется класс случайных (стохастических) фракталов. В этом случае свойство самоподобия (масштабной инвариантности) наблюдается лишь «в среднем», т. е. подобными являются не сами отсчеты сигнала, а, например, его КФ или ПРВ в разных временных масштабах. Три характерные особенности самоподобных процессов выражены в медленном убывании дисперсии, долгосрочной зависимости и флуктуационном характере спектра мощности таких процессов [25].
Рассмотрим дискретную случайную последовательность отсчетов:
![]() ,
,
где ![]() -
СВ с заданным законом распределения.
Будем предполагать, что все рассматриваемые
СП имеют ограниченную ковариацию
-
СВ с заданным законом распределения.
Будем предполагать, что все рассматриваемые
СП имеют ограниченную ковариацию ![]() и
следовательно дисперсию
и
следовательно дисперсию ![]() .
СП будет обладать свойством самоподобия,
если агрегированный процесс
.
СП будет обладать свойством самоподобия,
если агрегированный процесс ![]() -го
порядка
-го
порядка
 (5.6)
(5.6)
будет
иметь КФ ![]() совпадающую
с КФ
совпадающую
с КФ ![]() исходного
СП для любых
.
При выполнении данного условия можно
утверждать, что дисперсия агрегированного
процесса
исходного
СП для любых
.
При выполнении данного условия можно
утверждать, что дисперсия агрегированного
процесса ![]() убывает
согласно выражению
убывает
согласно выражению
![]() ,
(5.7)
,
(5.7)
т. е. дисперсия агрегированных процессов – средних выборок – уменьшается медленнее, чем величина, обратная размеру выборки. В результате в самоподобных процессах имеет место явление долгосрочной зависимости, которое приводит к расходимости КФ процесса:
![]() .
(5.8)
.
(5.8)
Наконец энергетический спектр самоподобных процессов описывается выражением
![]() .
(5.9)
.
(5.9)
Собственно эти соотношения и определяют название самоподобного процесса: корреляционные свойства такого процесса, усредненного на различных временных интервалах, остаются неизменными.
21. Основные принципы моделирования потока событий.
Пусть в какие-то моменты непрерывного времени наступают события. Этот процесс называется потоком событий. Моделирование потока событий сводится к моделированию моментов времени, в которые они происходят.
Наибольший интерес представляет пуассоновский поток событий. Его осн. свойства:
Независимость – каждое событие наступает независимо от того, наступали ли другие.
Ординарность – в один момент времени может произойти не более одного события.
Стационарность – вероятность наступления определенного количества событий на некотором интервале времени зависит только от его длины и не зависит от его положения на временной оси:
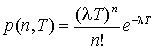
(
![]() –
интенсивность потока, т.е. ср. количествово
событий в единицу времени).
–
интенсивность потока, т.е. ср. количествово
событий в единицу времени).
Обозначим
![]() ,
,
![]() ,
... Тогда
,
... Тогда
![]() -
независимые случайные величины с
экспоненциальным распределением:
-
независимые случайные величины с
экспоненциальным распределением:
![]() .
.
Моделирование:
![]()
Как ранее было указано, вероятность того, что за интервал времени (t0, t0 + τ) произойдет m событий, определяется из закона Пуассона:


где a — параметр Пуассона.
Если λ(t) = const(t), то это стационарный поток Пуассона (простейший). В этом случае a = λ · t. Если λ = var(t), то это нестационарный поток Пуассона.
Для простейшего потока вероятность появления m событий за время τ равна:
![]()
Вероятность непоявления (то есть ни одного, m = 0) события за время τ равна:

22. Распределение Парето: математическое ожидание, дисперсия, абсолютные моменты, центральные моменты.