93. Расчет необходимого числа соединительных линий.

Предметом нашего рассмотрения будет телефонный коммутатор, который предназначен для концентрации абонентской нагрузки и передачи ее в сеть. Примером таких коммутаторов являются учрежденческие производственные АТС, называемые УПАТС, а в зарубежной литературе — РВХ (Private Branch exchange). Аналогичную методику расчетов можно применять и для расчета оконечных АТС городской телефонной сети. Поскольку задачей рассматри­ваемой системы является сбор нагрузки от подключенных к коммутатору внутренних абонентов, осуществление собственно коммутации внутренних звонков и передача от внешних абонентов к внутренним абонентам и обрат­но, то она может быть представлена как СМО, обслуживающая потоки заявок трех типов: внутренние, входящие и исходящие звонки. Нагрузка, создавае­мая всеми тремя типами звонков, обычно определяется на основе прошлого опыта построения подобных систем. В отечественной практике этот опытобобщен в руководящем документе РД 45.120-2000, принятом Министерст­вом связи и информатизации РФ в качестве основного нормативного доку­мента при проектировании сетей городской и сельской связи. В случае про­ектирования ведомственной сети требования могут быть иными, но анало­гичными.

Упомянутый документ содержит таблицу, в которой приводятся статистиче­ски средние характеристики звонков различного типа (табл. 6.1).

Далее, нужно проанализировать долю внутренних, внутристанционных звон­ков для того, чтобы исключить их из внешней нагрузки. В РД 45.120-2000 имеется таблица, позволяющая сделать это в зависимости от доли исходящей нагрузки.

Теперь, если необходимо, можно найти исходящую и входящую нагрузки раздельно и раздельно определить число входящих и исходящих линий по заданной норме потерь— вероятности блокировки. Упомянутый документ определяет нормативные потери таблицей, где данные приведены в десятых долях процента (табл. 6.2).

Проделанные расчеты, использующие Л-формулу Эрланга, приводят к сле­дующей таблице, определяющей нормативное число соединительных линий для подключения УПАТС к городской телефонной сети (табл. 6.3). Для меньшего числа абонентов сети РД предлагает эмпирическую формулу:

m = 4 + (N- 16)/8.

Очевидно, что она пригодна только для более шестнадцати абонентов. Посмотрим, как эта формула согласуется с известными нам формулами Эрланга и Энгсета. В соответствии с этими формулами число абонентских линий нужно рассчитывать так, чтобы выполнялось соотношение

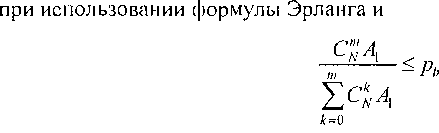
при использовании формулы Энгсета. В первом случае имеется суммарная внешняя нагрузка A_slim = NA\, а во втором — только удельная нагрузка^].

95. Анализ сетей массового обслуживания.

Сеть массового обслуживания представляет собой совокупность конечного числа N обслуживающих узлов, в которой циркулируют заявки, переходящие в соответствии с маршрутной матрицей из одного узла в другой. Узел всегда является разомкнутой СМО (причем СМО может быть любого класса). При этом отдельные СМО отображают функционально самостоятельные части реальной системы, связи между СМО  структуру системы, а требования, циркулирующие по СеМО,  составляющие материальных потоков (сообщения (пакеты) в коммуникационной сети, задания в мультипроцессорных системах, контейнеры грузопотоков и т.п.).Для наглядного представления СеМО используется граф, вершины которого (узлы) соответствуют отдельным СМО, а дуги отображают связи между узлами.

Классификация систем массового обслуживания.

Используется трех -, четырех -, шести – компонентное символическое обозначение системы массового обслуживания, предложенное Кендаллом (Candall) и развитое в работах Г.П.Барашина.

a/b/c :d/e/f

a – распределение поступающего потока запросов.

b – закон распределения времени обслуживания.

Типовые условные обозначения:

М – экспоненциальное (Марковское) распределение,

D – детерминированное распределение,

E^k – эрланговское распределение k-го порядка,

HM^k – гиперэкспоненциальное,

HE^k – гиперэрланговское распределение порядка k,

GI – произвольное распределение независимых промежутков между заявками,

G – произвольное распределение длительностей обслуживания.

c – структура системы обслуживания (обычно число серверов).

d – дисциплина обслуживания (параметры после двоеточия иногда опускают).

Обычно используется сокращенное символическое обозначение, например FF вместо FIFO, LF, PR и т.п.

e – максимальное число запросов, воспринимаемое системой, может употребляться символ .

f – максимальное число запросов к системе обслуживания.

В некоторых публикациях последними символами отражают качественные характеристики системы обслуживания. Некоторые общие результаты и основы математического аппарата, необходимого для анализа можно получить, рассматривая системы G/G/m.