68. Непрерывные цепи Маркова.

69.Анализ системы «гибели-размножения». Графическая интерпретация процессов переходов в непрерывной цепи Маркова.

в каждом из серверов. Если ввести функцию in(7), численно равную количе­ству входных требований, поступивших в систему в интервал времени t + dt, то формально уравнения эволюции системы во времени могут быть описаны следующим образом:

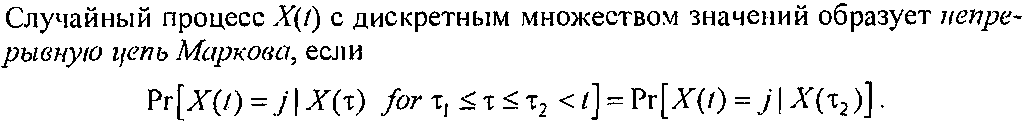
Это означает, что в каждый последующий момент времени распределение вероятностей состояния системы зависит только от предыдущего состояния и входного потока.

суммарное число требований в очереди и в сервере: k = N_q+N_s и записать уравнение состояний в виде:

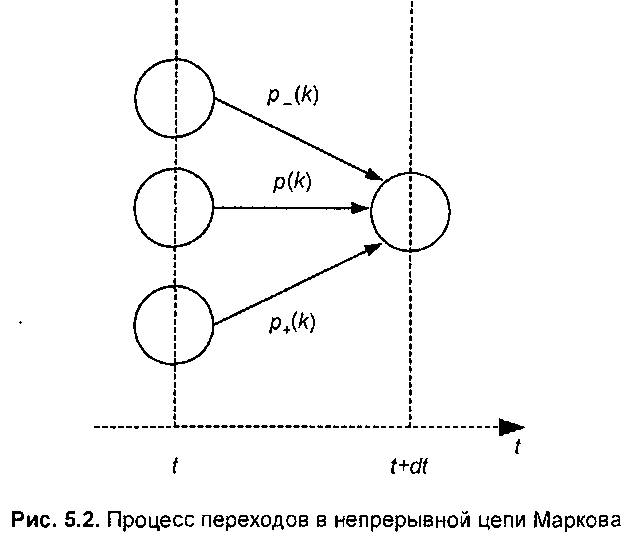
Конкретизация вида функции в правой части может быть получена из простых соображений. Система, которую мы рассматриваем, может интер­претироваться в терминах биологического плана как некоторая популяция, численностью к, в которой в каждый малый интервал времени с заданной вероятностью способен либо появиться новый экземпляр (рождение члена популяции), либо исчезнуть ровно один экземпляр с заданной вероятностью. Альтернативой может быть сохранение численности на этом интервале неиз­менной. В литературе такую систему называют процессом "гибели-размно­жения". На рис. 5.2 приведена графическая иллюстрация поведения описан­ной системы.

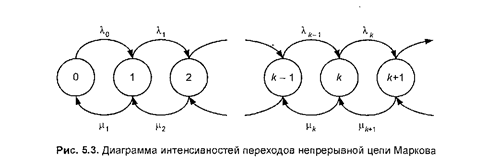
70. Диаграмма интенсивностей переходов для непрерывной цепи Маркова.

В соответствие этой системе уравнений можно поставить наглядную диа­грамму интенсивностей переходов, которая аналогична диаграмме переходов для дискретных цепей Маркова (рис. 5.3).

Окружностям здесь соответствуют дискретные состояния, а дуги определяют интенсивности потоков вероятности (а не вероятности!) переходов от од­ного состояния к другому.

71.Уравнения равновесия или баланса.

Имеет место своеобразный "закон сохранения"-, разность между интенсив­ностью, с которой система попадает в состояние к, и интенсивностью, с кото­рой система покидает это состояние, должна равняться интенсивности изме­нения потока в это состояние (производной по времени).

Применение закона сохранения позволяет получать уравнения для любой подсистемы марковской цепи типа процесса "гибели-размножения". Особен­но эффективным оказывается построение решений в стационарном, устано­вившемся режиме, когда можно полагать, что вероятности в произвольный, достаточно отдаленный момент времени, остаются постоянными.

Приравнивая производную по времени нулю, получаем систему разностных уравнений:

Система, описываемая полученными выше выражениями, будет иметь ста­ционарные вероятности состояний, когда она эргодическая. Это условие мо­жет быть выражено через соотношение интенсивностей. Необходимо и дос­таточно, чтобы существовало некоторое значение к, начиная с которого вы­полнялось бы неравенство

Для большинства реальных систем массового обслуживания это неравенство выполняется.

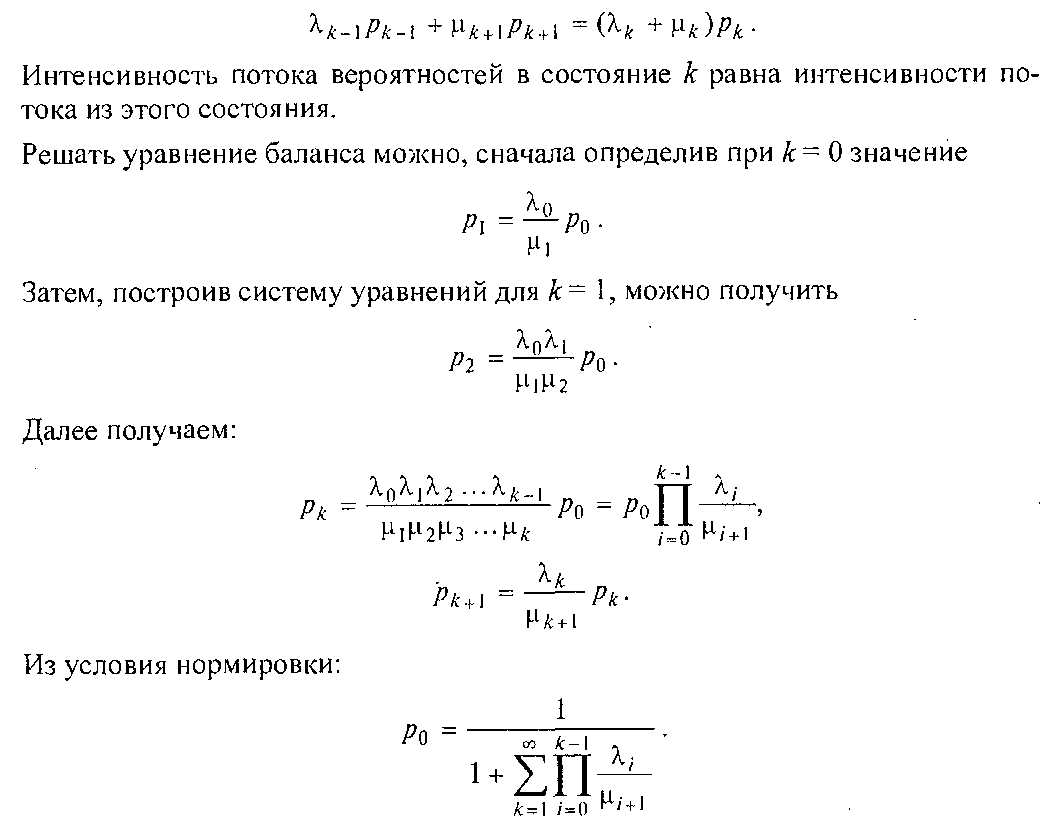
Таким образом, нам удалось построить математическую модель, описываю­щую весьма широкий класс СМО, для которой найдено решение в замкнутой форме.