
- •1 Основные понятия и определения
- •2 Принципы управления
- •3 Классификация систем управления
- •4. Системы автоматической стабилизации, программного управления и следящие сау.
- •6. Математическое описание сау. Дифференциальные уравнения.
- •7Математическое описание. Преобразование Лапласа. Передаточная функция.
- •8 Математическое описание. Частотные характеристики.(афчх, лах и лфх)
- •10 Математическое описание. Временные характеристики.
- •39 Передаточные функции разомкнутой, замкнутой сау и ошибки регулирования.
- •20 Критерии устойчивости. Критерий Гурвица.
- •21 Критерии устойчивости. Критерий Найквиста.
- •22 Критерии устойчивости. Критерий Михайлова.
- •23 Критерии устойчивости. Определение устойчивости по логарифмическим характеристикам.
- •25 И 26 Точность сау. Статические и астатические системы.
- •1) Ступенчатое воздействие.
- •27 Оценка качества регулирования.
- •27 Оценка качества регулирования по частотным характеристикам
- •27 Построение желаемой лах.
- •19 Понятие устойчивости сау.
- •28 Виды корректирующих устройств.
- •31И 30 Нелинейные сау. Типовые нелинейные звенья.
- •30 Основные различия между линейными и нелинейными системами.
- •34 Устойчивость нсау. Метод гармонического баланса.
- •33 Устойчивость нсау. Абсолютная устойчивость. Критерий Попова.
- •36И37 Импульсные сау. Виды квантования.
- •39 Передаточные функции разомкнутой и замкнутой импульсной сау.
- •24. Запасы устойчивости
- •35 Устойчивость автоколебаний.
- •.29 Типовые желаемые лачх.
39 Передаточные функции разомкнутой, замкнутой сау и ошибки регулирования.
Характеристические уравнения систем
Типовая структура замкнутой САУ, передаточная функция и характеристическое уравнение разомкнутой системы.

![]() – передаточная
функция разомкнутой системы.
– передаточная
функция разомкнутой системы.
Для линейных систем применим принцип суперпозиции воздействий (независимых воздействий).
![]() -
Передаточная функция замкнутой системы
относительно регулирующей величины по
задающему воздействию.
-
Передаточная функция замкнутой системы
относительно регулирующей величины по
задающему воздействию.

![]() – передаточная
функция замкнутой системы относительно
задающей величины по возмущающему
воздействию.
– передаточная
функция замкнутой системы относительно
задающей величины по возмущающему
воздействию.
![]() – передаточная
функция замкнутой системы относительно
ошибки регулирования, по задающему
воздействию.
– передаточная
функция замкнутой системы относительно
ошибки регулирования, по задающему
воздействию.
![]() – передаточная
функция замкнутой системы относительно
ошибки регулирования, по возмущающему
воздействию.
– передаточная
функция замкнутой системы относительно
ошибки регулирования, по возмущающему
воздействию.
![]() – передаточная
функция разомкнутой системы
– передаточная
функция разомкнутой системы
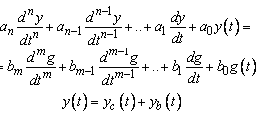
![]() –
Характеристическое
уравнение разомкнутой системы получается
приравниванием к нулю знаменателя
передаточной функции разомкнутой
системы.
–
Характеристическое
уравнение разомкнутой системы получается
приравниванием к нулю знаменателя
передаточной функции разомкнутой
системы.
Для нахождения характеристического уравнения замкнутой системы необходимо также приравнять к нулю знаменатель передаточной функции замкнутой системы

Характеристическое уравнение замкнутой системы может быть получено приравниванием к 0 суммы числителя и знаменателя передаточной функции разомкнутой системы.
20 Критерии устойчивости. Критерий Гурвица.
Устойчивость – свойство САУ возвращаться в заданный или близкий ему установившийся режим после какого-либо воздействия.
САУ устойчива, если переходные процессы в ней затухающие, выходная величина является ограниченной при условии, что входная величина также ограничена.
Критерий устойчивости Гурвица:
Пусть D(p) = a0pn + a1pn-1 + … + an, тогда:
 -
определитель Гурвица
-
определитель Гурвица
Для того, чтобы система была устойчива необходимо и достаточно, чтобы ∆n и все его миноры были положительны при a0>0.
21 Критерии устойчивости. Критерий Найквиста.
Относится к частотным критериям и позволяет судить об устойчивости замкнутой системы по виду годографа АФХ разомкнутой системы.
Передаточная
функция замкнутой системы –
![]()
Передаточная
функция разомкнутой системы –
![]()

Разомкнутая система в общем случае может быть не устойчива. Но если она устойчива в замкнутом состоянии, то этого достаточно для ее работоспособности.
(-n+2l)π/2= l*π
Для устойчивости замкнутой линейной системы n-го порядка необходимо и достаточно, чтобы при изменении частоты от 0 до ∞, изменение фазы частотной функции D(jw) равной 1+W(jw) равнялась l*π, где l – число правых корней характеристического уравнения разомкнутой системы.
Вспомогательную частотную функцию W(jw) на 1 отличающуюся от амплитудно фазовой характеристики разомкнутой системы можно рассматривать как АФХ при смещении оси ординат на -1.
На практике такого смещения не делают, а рассматривают изменение фазы функции D(jw) как изменение фазы вектора, проведенного из точки с координатами (-1;j0) к годографу АФХ разомкнутой системы.
При изменении частоты до ∞ конец этого вектора скользит по годографу АФХ разомкнутой системы.
Формулировка критерия:
1) Общий случай: для устойчивости замкнутой системы n-го порядка необходимо и достаточно, чтобы изменение фазы вектора проведенного из точки (-1;j0) к годографу АФХ разомкнутой системы при изменении частоты в интервале от 0 до ∞ было равно l*π, где l – число правых корней характеристического уравнения разомкнутой системы.
2) Частный случай 1: если в разомкнутом состоянии система устойчива, тогда для устойчивости системы необходимо и достаточно, чтобы годограф АФХ разомкнутой системы не охватывал точку (-1;j0)
3) Частный случай 2: Особенности применения критерия Найквиста для астатических систем.
При оценке устойчивости астатических систем необходимо учитывать фазовый сдвиг определяемый левыми корнями характеристического уравнения, чтобы исключить влияние интегрирующих звеньев необходимо при w>0 достроить АФХ разомкнутой системы дугой ∞-о большого радиуса ν*π/2 против часовой стрелки, где ν – порядок астатизма системы – число интегрирующих звеньев. Далее применяем критерий Найквиста в обычной интерпретации.
На рисунках 3,19 и 3,20 запас устойчивости.
