6. Математическое описание сау. Дифференциальные уравнения.

Дифференциальная и операторная формы линейных ДУ.

Запись дифференциальных уравнений в операторной форме позволяет свести задачу к решению системы алгебраических уравнений. К x(t) и g(t) можно применить преобразование Лапласа.

В результате применения преобразования Лапласа можем перейти от дифференциального уравнения к алгебраическому уравнению.

После преобразования имеем следующую схему:

Уравнение САУ позволяет по x(t) найти g(t) и наоборот

– полином входа

– полином выхода

Чем сложнее полином, тем сложнее система

W(p) – передаточная функция

7Математическое описание. Преобразование Лапласа. Передаточная функция.

Анализ и синтез САУ существенно упрощается при использовании прикладных математических методов операционного исчисления.

Имеется функция вещественной переменной f(t), ей можно поставить в соответствие F(p), где f(t) – оригинал, F(p) – изображение.

-интеграл Лапласа

– комплексная переменная;

Преобразование Лапласа обладает следующими свойствами: операциям дифференцирования и интегрирования в приведении вещественной переменной соответствуют эквивалентные алгебраические операции умножения и деления с использованием комплексной переменной.

Применение преобразования Лапласа позволяет перейти от исходных дифференциальных уравнений к эквивалентным алгебраическим уравнениям в представительстве комплексной переменной.

Передаточной функция звена или системы – отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях.

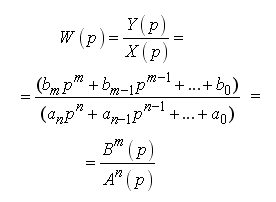– передаточная функция.

8 Математическое описание. Частотные характеристики.(афчх, лах и лфх)

Если на вход звена (системы) подать гармоническое воздействие , то после окончания переходных процессов на выходе устанавливаются колебания той же частоты, но иной амплитуды и сдвинутые по фазе относительно входных колебаний.

– амплитудно-фазовая характеристика есть отношение выходной величины к входной величине выраженной в комплексной форме.

– АЧХ

– функция частоты – ФЧХ

АФХ может быть получена из выражения передаточной функции W(p) заменой комплексной переменной р на мнимую переменную jw:

АФХ строится на комплексной плоскости в координатах вещественная составляющая по оси х; мнимая составляющая по оси у, при изменении частоты от 0 до ∞.

10 Математическое описание. Временные характеристики.

Временная характеристика звена системы – закон изменения выходной величины в функции времени при изменении входной величины по определенному закону и при условии, что до приложения внешнего воздействия звено находилось в покое. Зависит от характера звена.

Ступенчатое воздействие при t=0,входная величина X

Линейное воздействие с постоянной скоростью

Переходная функция звена – реакция звена на единичное ступенчатое воздействие.

Y(p)=W(p)*X(p); H(p)=>W(p)/p; L{1(t)}=1/p; h(t)=L^-1[W(p)/p]

Импульсная переходная или весовая функция – реакция звена на импульсное воздействие в виде δU

Y(p)=W(p)*X(p); L[δ(t)]=1; K(p)=W(p)*1; k(t)=L^-1[W(p)]; W(p)=pH(p)=k(p); k(t)=dh/dt

Достоинством временных характеристик является то, что они могут быть получены экспериментально.

11 Элементарные типовые звенья. Интегрирующее звено.

Так называют звено с передаточной функцией W(s) = к/s. Его частотные и временные функции имеют следующий вид:

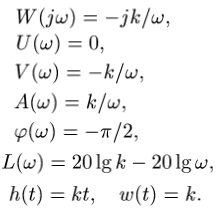
АФЧХ:

ЛАХ, ЛФХ:

Переходная характеристика:

k-коэфф усиления

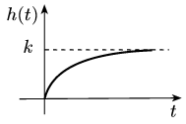
12 Элементарные типовые звенья. Апериодическое звено.

Так называют звено с передаточной функцией W(s) = k/(Ts + 1). Его частотные и временные функции имеют следующий вид:

АФЧХ:

ЛАХ, ЛФХ:

Переходная характеристика:

13 Элементарные типовые звенья. Колебательное звено.

Так называют звено с передаточной функцией:

АФЧХ:

ЛАХ,ЛФХ:

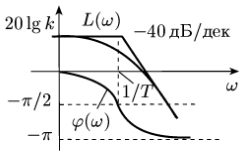
Переходная характеристика:

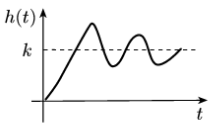
15 Элементарные типовые звенья. Дифференцирующее звено I-го порядка.

Передаточная функция:

W(p)=k(Tp+1)

16 Элементарные типовые звенья. Дифференцирующее звено II-го порядка.

Передаточная функция:

W(p)=k(T²p²+2ETp+1)

14 Элементарные типовые звенья. Идеальное дифференцирующее звено.

Дифференцирующее звено. Так называют звено с передаточной функцией W(s) = ks. Его частотные и временные функции имеют следующий вид:

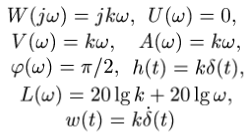
АФЧХ:

ЛАХ, ЛФХ:

17 Преобразование структурных схем САУ. Связь структурных схем с графами.

Л юбую САУ можно рассматривать как комбинацию динамических звеньев. Изображение САУ в виде совокупности динамических звеньев с указателями связей между ними назыв. структурной схемой. 1) звено с 1 входом и выходом для него Y(p)=W(p) *X(p) 2) звено с 2-мя входами

д ля него Y(p)=W1(p)*X1(p)+ W(p)*X2(p). Его можно представить и в другом виде:

3) Узел х1=х2=х3

4) Сумматор y=x1±x2

или или

П равило преобраз. структурных схем: 1) перестановка однотипных элементов: а) узлы с узлами, б) сумматоры с сумматорами, в) звенья со звеньями:

= 2) Перенос узла череззвено: а) с выхода на вход б) со входа

на выход =

=

3

W1

Х1

Х3

) Перенос сумматора через звено: а) со входа на выход б) с выхода на вход =

Х2

С

W(р)

х

у

труктурные схемы САУ могут быть изображены в виде сигнальных графов. Def Графом назыв. множество вершин и ребер. Каждому ребру соотв. 2 вершины: начало и конец ребра. Каждая вершина отмеченная на графе кружком или точкой соотв. некоторой переменной рассматр. системы. Каждое ребро изображается в виде линии со стрелкой указывающее направление прохождения сигнала, имеет вершину начало вход. вел. и вершину конец выходной вел. Между структурной схемой и графом имеется след-е соотв-е: прямоуг-к структ-ой схемы соотв. ребру графа, а стрелки на структ-й схеме соотв. вершинам графа его граф

П ример: