24. Запасы устойчивости

В процессе эксплуатации САУ ее параметры (коэффициенты усиления, постоянные времени) из-за из­менения внешних условий, колебаний напряжений источ­ников энергии и других причин отличаются от расчетных значений. Если не принять определенных мер, то исходная устойчивая система  может стать неустойчивой. Для исключения этого явления при проектировании следует обеспечить опреде­ленные запасы устойчивости системы, которые характе­ризуют близость годографа амплитудно-фазовой  характе­ристики разомкнутой системы   W(jω)  к точке с координатами (-1, j0).

Различают запас устойчивости по фазе и усилению. Запасы устойчивости определяются на двух частотах: частоте среза ω_с и критической частоте ω_кр . На частоте среза амплитудно-частотная характеристика разомкнутой системы  |W(jω)| равна единице, а на критичес­кой частоте фазо-частотная характеристика этой системы φ(ω) принимает значение, равное -π.

Запас устойчивости по фазе Δφ показывает, насколько фазо-частотная характеристика разомкнутой системы на частоте среза ω_с отлича­ется от  -π  (рис. 3.9):

Δφ =  π – .

Величина запаса устойчивости по усилению может быть определена на частоте ω_кр, как разность:

      =  1 – |W(jω_кр)|,

либо как отношение

α  =  1/ |W(jω_кр)|.

Во втором случае величина запаса устойчивости по усилению определяет,  во сколько раз необходимо увеличить коэффициент усиления, чтобы система оказалась на границе устойчивости.

Системы, годографы W(jω) ко­торых пересекают вещественную ось только справа от точки с координатами (-1, j0) (рис. 3.10, а), называют аб­солютно устойчивыми. В таких системах неустойчивость может наступить только при увеличении коэффициента усиления.

Если годограф частотной характеристики W(jω) разомкну­той системы пересекает вещественную ось и слева от точ­ки с координатами (-1, j0), то систему называют услов­но устойчивой (рис. 3.10, б). Неустойчивой такая система может быть как при увеличении, так и при уменьшении коэффициента усиления.

Для нормальной работы САУ необходимо, что­бы запас устойчивости по усилению α был не менее двух, а запас устойчивости

35 Устойчивость автоколебаний.

Можно показать, что для устойчивости автоколебаний, то есть, чтобы их амплитуда, частота и форма были устойчивы к малым возмущениям начальных условий необходимо выполнение условия:

(25)

Условие (25), так же, как и условия (21,22) является лишь необходимым, то есть позволяет отсеять заведомо неустойчивые автоколебания.

.29 Типовые желаемые лачх.

К ак уже отмечалось ранее, важным требованием к САУ в динамике является условие , чтобы САУ отрабатывала управляющее воздействие в минимально возможное время и с наименьшей колебательностью и не реагировала на возмущающее воздействия.

Пусть имеется САР, у которой существует однозначная зависимость между ЛАЧХ и ЛФХ (минимально-фазовая САР) вида:

Заданную структурную схему можно преобразовать к виду:

т.е. по заданию по возмущению

а)

б) для зависимостей

в) для ЛАЧХ замкнутой САР

г) для ЛАЧХ системы в разомкнутом состоянии

; ;

т.н. betrags оптиум (оптиум с однократным интегрированием)

,

где Т сумма малых пост. времени

Таким образом желаемая характеристика находится:

Поскольку основную роль играет

ЛАХ в районе частоты среза, то в некоторых случаях для предварительного выбора Lр жел. используется следующая методика:

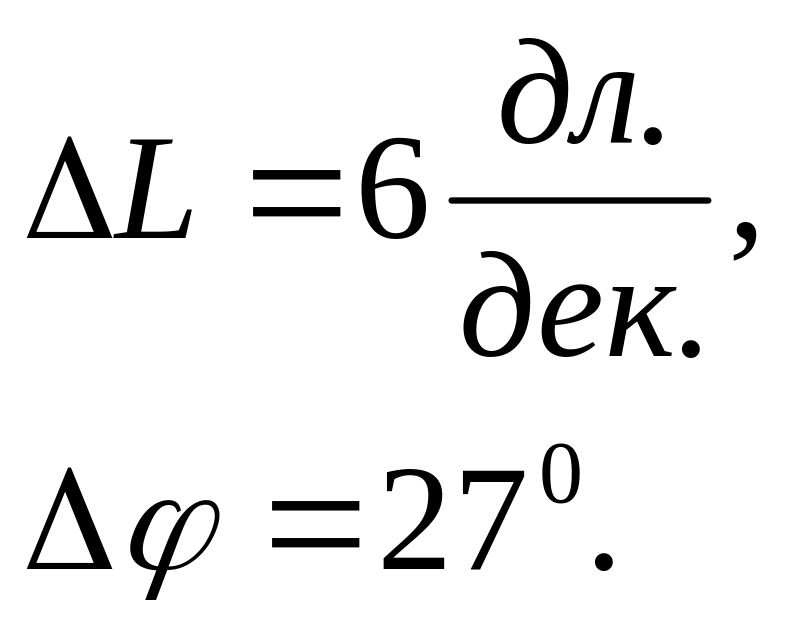
т.е. используется т.н. симметричный оптиум с 2-х кратным интегрированием

при этом W

где Т -сумма малых постоянной времени рассматриваемой САР.

7