7 Вопрос

7,1 Пересечение прямой с плоскостью.

Если прямая не лежит в плоскости и не параллельна ей, она пересекает плоскость. Задача на определение точки пересечения прямой с плоскостью сводится к следующему: 1) проведению вспомогательной плоскости (Вспомогательную плоскость рекомендуется выбирать такую, которая даст наиболее простое графическое решение задачи) через данную прямую; 2) нахождению линии пересечения вспомогательной плоскости с данной плоскостью; 3) определению точки пересечения данной прямой с линией пересечения плоскостей, а следовательно, с данной плоскостью.

Пересечение прямой с проектирующей плоскостью. Пример 1. На (фиг.250,а) даны плоскость δ (δ₁) и прямая АВ (А₁В₁ и А₂В₂); требуется определить точку их пересечения.

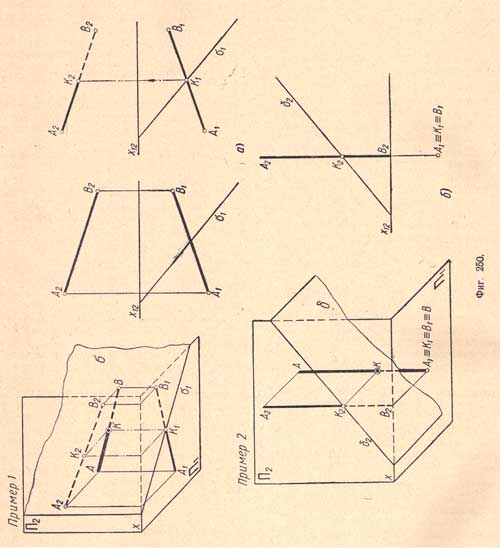
В этом случае нет надобности прибегать к вспомогательной плоскости, так как данная плоскость δ - горизонтально - проектирующая. По свойству проектирующих плоскостей горизонтальная проекция точки пересечения, лежащая в плоскости δ, сливается с горизонтальной проекцией δ₁. Поэтому точка К₁ пересечения горизонтальной проекции А₁В₁ прямой АВ с горизонтальной проекцией δ₁ есть горизонтальная проекция точки пересечения К; фронтальная проекция К₂ определяется путем проведения вертикальной линии связи до пересечения ее с фронтальной проекциейА₂В₂. Пример 2. На (фиг.250,б) приведен пример пересечения прямой АВ с фронтально - проектирующей плоскостью δ.

Пересечение прямой с плоскостью общего положения. Пример 1. Даны: плоскость общего положения а и прямая общего положенияАВ (А₁В₁ А₂В₂); требуется найти точку их пересечения (фиг.251,а). Проводим через прямую АВ какую - либо вспомогательную плоскость, например горизонтально - проектирующую плоскость δ (δ₁), как показано на (фиг.251,б); она пересечет плоскость a по прямой NM (N₁M₁, N₂М₂), которая, в свою очередь, пересечет прямую АВ (А₁В₁ А₂В₂) в точке С (С₁С₂), что видно на (фиг.251,в). Точка С есть точка пересечения прямой АВ с плоскостью а.

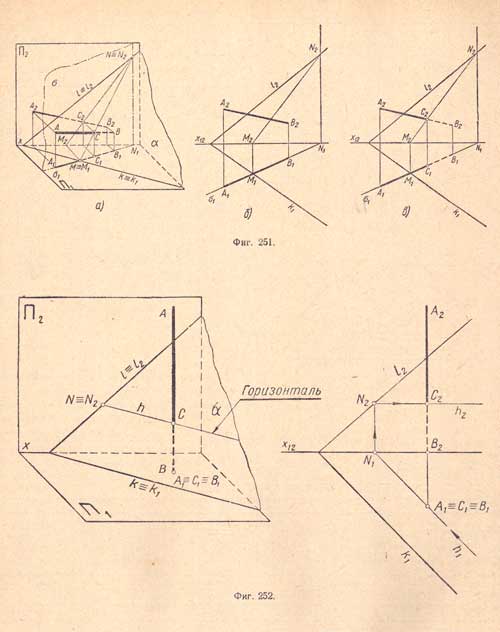
Пример 2. На (фиг.252) приведен пример нахождения проекций точки пересечения прямой AB c плоскостью общего положения при помощи горизонтали h. Пример 3. Даны: треугольник ABC и прямая NM; требуется определить точку их пересечения (фиг.253,а). Возьмем в качестве вспомогательной плоскости горизонтально - проектирующую плоскость δ, тогда горизонтальная проекция ог сольется с горизонтальной проекцией N₁M₁ прямой NM и пересечет проекции сторон треугольника в точках Е₁ и F₁ (фиг.253,б). Отрезок Е₁F₁ будет горизонтальной проекцией линии пересечения. Затем находим фронтальную проекцию линии пересечения: при помощи вертикальных линий связи получаем точкиЕ₂ и F₂, проводим через них прямую E₂F₂, которая будет фронтальной проекцией линии пересечения. Прямая E₂F₂ пересекает прямую N₂М₂ в точке К₂. Точка К₂ будет фронтальной проекцией точки пересечения прямой MN с прямой EF; горизонтальную проекцию K₁ этой точки определяем при помощи вертикальной линии связи. Точка К (K₁, К₂) будет точкой пересечения данной прямой MN с данным треугольником ABC, как одновременно им принадлежащая, потому что прямая MN пересекается в ней с прямой EF, лежащей в плоскости треугольника ABC.

7,2 ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПОВЕРХНОСТЯМИ ГЕОМЕТРИЧЕСКИХ ТЕЛ При пересечении прямой с поверхностью тела получаются две точки, одновременно принадлежащие как прямой, так и поверхности тела. Эти точки называются точками входа и выхода. Для нахождения этих точек в общем случае поступают так: 1) проводят через данную прямую проектирующую плоскость; 2) находят фигуру сечения данной плоскостью; 3) определяют точки пересечения прямой с контуром сечения. Разберем сказанное на примере (фиг.323). Надо найти точки пересечения прямой d с поверхностью неправильной пирамиды.

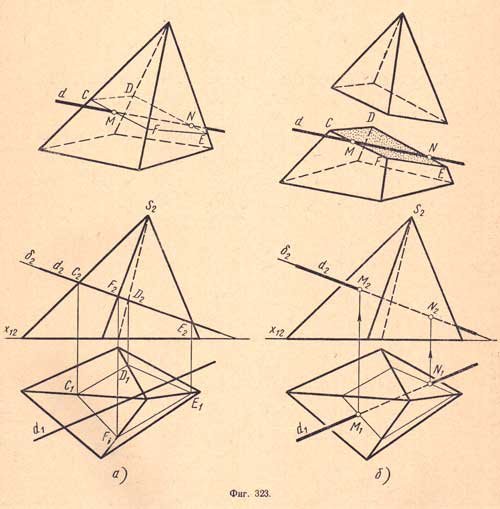
Проведем через прямую d фронтально - проектирующую плоскость δ. Проекция δ₂ совпадает с фронтальной проекцией δ₂. В сечении получим четырехугольник, его горизонтальная проекция C₁D₁E₁F₁выявится четырехугольником, а фронтальная (C₂F₂D₂E₂) - отрезком прямой, сливающимся с проекцией δ₂ (фиг.323,а). Пересечения горизонтальной проекции d₁ прямой с проекциями C₁F₁ и D₁E₁сторон четырехугольника - точки М₁ и N₁ - являются горизонтальными проекциями точек пересечения прямой d с поверхностью пирамиды. Фронтальные проекции М₂ и N₂ находят при помощи вертикальных линий связи (фиг.323,б).

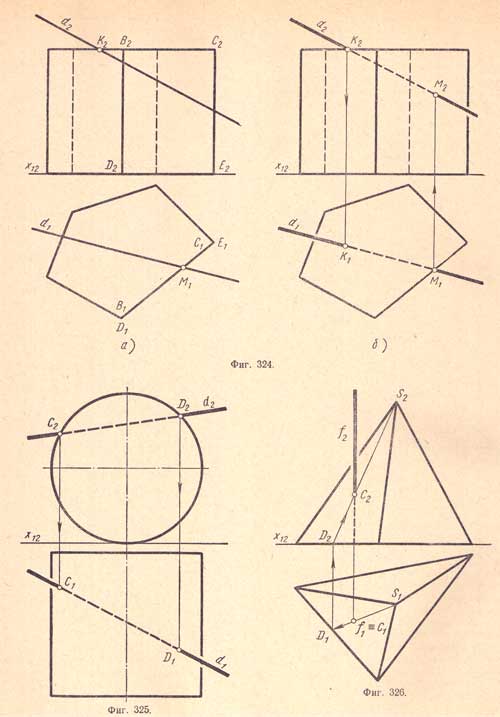
В тех частных случаях, когда грани тела или поверхность тела вращения перпендикулярны одной из плоскостей проекцией, применять вспомогательные проектирующие плоскости нецелесообразно, так как одна из проекций точек входа и выхода уже выявлена на чертеже. На (фиг.324,а) даны проекции прямой призмы и прямой d, которая пересекает верхнее основание призмы и ее боковую грань BCED (B₁C₁E₁D₁ иB₂C₂E₂D₂). Точка К₂ является фронтальной проекцией пересечения основания; точка М₁ - горизонтальной проекцией пересечения грани BCEDданной линией. Горизонтальная проекция К₁ и фронтальная проекция М₃точек пересечения находятся при помощи вертикальных линий связи (фиг.324,б). На (фиг.325) показан пример пересечения прямой d с поверхностью прямого кругового цилиндра. Точки С₂ и D₂ выявлены как фронтальные проекции точек пересечения; горизонтальные проекции С₁ и D₁ найдены при помощи вертикальных линий связи. В тех частных случаях, когда прямая, пересекающая поверхность тела, перпендикулярна одной из плоскостей проекций, определение проекций точек пересечения аналогично предыдущему. На (фиг.326) показан пример такого случая. Прямая f, пересекающая поверхность пирамиды, перпендикулярна плоскости проекций П₁. Горизонтальная проекция точки пересечения выявлена на чертеже точкой C₁сливающейся с горизонтальной проекцией f₁ прямой; фронтальная проекцияС₂ найдена посредством вспомогательной прямой SD. Несколько иначе решается задача определения проекций точек пересечения прямой с ша-ровой поверхностью. На (фиг.327) показано такое решение. Прямая d общего положения пересекает шаровую поверхность; для определения точек пересечения, кроме проектирующей плоскости, применен метод перемены плоскостей проекций.

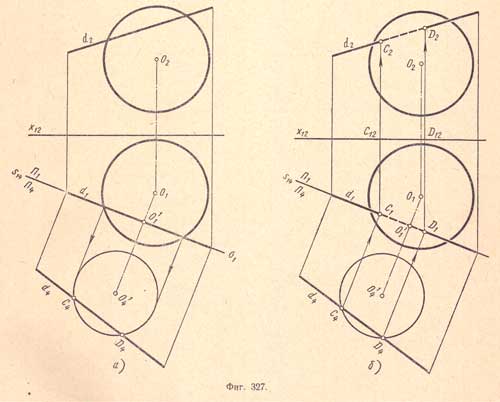Проведем через прямую d горизонтально-проектирующую плоскость δ. Проекция δ₁ совпадает с горизонтальной проекцией d₁. В сечении получим окружность. Примем плоскость δ за новую плоскость проекций и спроектируем на нее прямую и окружность сечения; так как прямая и сечение лежат в плоскости δ, то они спроектируются на нее в натуральную величину. Новая проекция d₄ прямой пересекает контур фигуры сечения - окружность - в точках C₄ и D₄; они являются искомыми точками пересечения (фиг.327,а). Обратным проектированием сначала находим горизонтальные проекции C₁и D₁ искомых точек пересечения, а затем соответствующие им фронтальные проекции С₂ и D₂ (фиг.327,б). Нахождение точек пересечения прямой общего положения с поверхностью конуса решается при помощи вспомогательной плоскости, проходящей через заданную прямую и вершину конуса. Для примера возьмем прямой круговой конус и прямую d общего положения, пересекающую его коническую поверхность (фиг.328). Для определения точек пересечения достаточно вершину конуса S соединить прямой с произвольной точкой Q, находящейся на прямой d, найти горизонтальный след этой прямой и данной прямой d. Соединяя проекции следов М₁ и М₁¹ прямой, получим проекцию k₁горизонтального следа k вспомогательной плоскости а, которая пересечет конус по двум образующим SC и SD (фиг.328,а).

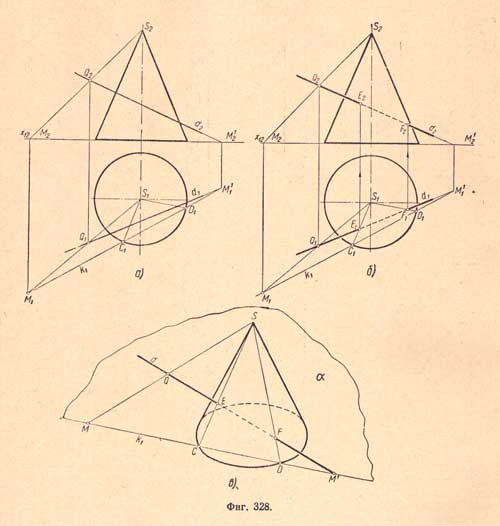Пересечение горизонтальной проекции d₁ с проекциями образующих дает горизонтальные проекции E₁ и F₁ искомых точек. Затем при помощи линий связи находим фронтальные проекции E₂ и F₂ (фиг.328,б).