Вопрос 34

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.

Геометрический и физический смысл производной

Тангенс угла наклона касательной прямой

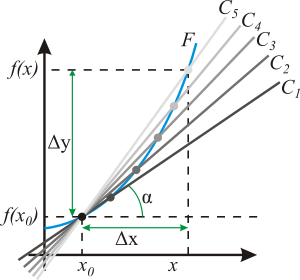
Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точкиx₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную(постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Если функция   имеет конечную производную в точке   то в окрестности   её можно приблизить линейной функцией

Функция   называется касательной к   в точке   Число   является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции

Пусть   — закон прямолинейного движения. Тогда   выражает мгновенную скорость движения в момент времени   Вторая производная   выражает мгновенное ускорение в момент времени 

Вообще производная функции   в точке   выражает скорость изменения функции в точке  , то есть скорость протекания процесса, описанного зависимостью 

Вопрос 35

Дифференцирование – вычисление производных и дифференциалов любого порядка от функции одного переменного и частных производных и дифференциалов, а также полных дифференциалов от функций многих переменных.

Операция дифференцирования обладает свойством линейности: будучи примененной к линейной комбинации дифференцируемых функций f₁, f₂, …, f_n c числовыми коэффициентами с₁; с₂; …; с₂, т.е. к выражению

с₁f₁ + c₂f₂ + … + c_nf_n,

она дает такую же линейную комбинацию (т.е. линейную комбинацию с теми же коэффициентами)  производных или дифференциалов соответственно.

Основные правила дифференцирования. Сумма.

      Выведем несколько правил вычисления производных, В этом пункте значения функций u и v и их производных в точке х₀обозначаются для краткости так: u(х₀) = u, v(х₀) = v, u'(х₀) = u', v'(х₀)=v`. Если функции u и v дифференцируемы в точке х₀, то их сумма дифференцируема в этой точке и

(u+v)' = u' + v'.

      Коротко говорят: производная суммы равна сумме производных.        1) Для доказательства вычислим сначала приращение суммы функций в рассматриваемой точке: Δ(u+v) = u (х₀+Δx)+ v(х₀+Δx) – (u(х₀)+v(х₀)) = (u(х₀+Δx)-u(х₀)) + (v(х₀+Δx)-v(х₀)) = Δu + Δv        2)

      3) Функции u и v дифференцируемы в точке х₀, т. е. при Δх→0 

      Тогда 

при Δх→0 (см. правило 3, а) предельного перехода), т. е. (u+v)' = u'+v’