Вопрос 30

Предел функции. Число L называется пределом функции  y = f ( x ) при  x, стремящемся к  a :

если для любого    > 0 найдётся такое положительное число   =   (   ), зависящее от   , что из условия | x  a | <  следует  |  f ( x ) – L | < 

Это определение означает, что L есть предел функции  y = f ( x ), если значение функции неограниченно приближается к  L , когда значение аргумента  x приближается к  a. Геометрически это значит, что для любого    > 0  можно найти такое число   , что если  x  находится в интервале ( a  a  ), то значение функции лежит в интервале ( L  ,  L +  ). Отметим, что в соответствии с этим определением аргумент функции лишь приближается  к  a , не принимая этого значения! Это следует учитывать при вычислении предела любой функции в точке её разрыва, где функция не существует.

Вопрос 31 Основные неопределенности пределов и их раскрытие.

С непосредственным вычислением пределов основных элементарных функций разобрались.

При переходе к функциям более сложного вида мы обязательно столкнемся с появлением выражений, значение которых не определено. Такие выражения называют неопределенностями.

Перечислим все основные виды неопределенностей: ноль делить на ноль   (0 на 0), бесконечность делить на бесконечность  , ноль умножить на бесконечность  , бесконечность минус бесконечность  , единица в степени бесконечность  , ноль в степени ноль  , бесконечность в степени ноль  .

ВСЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.

Раскрывать неопределенности позволяет:

• упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);

• использование замечательных пределов;

• применение правила Лопиталя;

• использование замены бесконечно малого выражения ему эквивалентным(использование таблицы эквивалентных бесконечно малых).

Сгруппируем неопределенности в таблицу неопределенностей. Каждому виду неопределенности поставим в соответствие метод ее раскрытия (метод нахождения предела).

Эта таблица вместе с таблицей пределов основных элементарных функций будут Вашими главными инструментами при нахождении любых пределов.

Разберем на примерах с подробными решениями раскрытие неопределенностей преобразованием выражений.

Очень часто выражение под знаком предела нужно немного преобразовать, чтобы избавиться от неопределенностей.

Пример.

Вычислить предел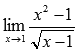 

Решение.

Подставляем значение:

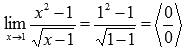
Пришли к неопределенности. Смотрим в таблицу неопределенностей для выбора метода решения. Пробуем упростить выражение.

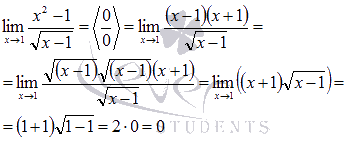
После преобразования неопределенность раскрылась.

Ответ:

Пример.

Вычислить предел 

Решение.

Подставляем значение:

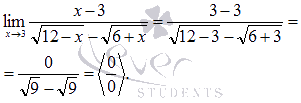
Пришли к неопределенности (0 на 0). Смотрим в таблицу неопределенностей для выбора метода решения и пробуем упростить выражение. Домножим и числитель и знаменатель на выражение, сопряженное знаменателю.

Для знаменателя сопряженным выражением будет 

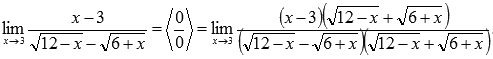
Знаменатель мы домножали для того, чтобы можно было применить формулу сокращенного умножения – разность квадратов и затем сократить полученное выражение.

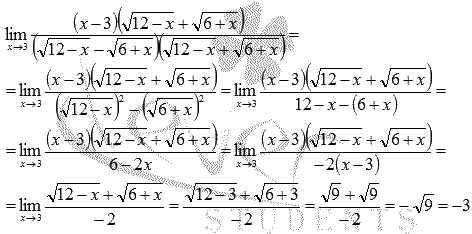
После ряда преобразований неопределенность исчезла.

Ответ:

ЗАМЕЧАНИЕ: для пределов подобного вида способ домножения на сопряженные выражения является типичным, так что смело пользуйтесь.