3.9. Общие теоремы динамики при ударе Краткие сведения по теории

Явление удара.

Ударом будем называть кратковременное действие на тело некоторой силы  . Силы, возникающей, например, при встрече двух массивных тел.

Опыт показывает, что взаимодействие их очень кратковременно (время контакта исчисляется тысячными долями секунды), а сила удара довольно велика (в сотни раз превышает вес этих тел). Да и сама сила – не постоянна по величине. Поэтому явление удара - сложный процесс, сопровождающийся к тому же деформацией тел. Точное исследование его требует знания физики твердого тела, законов тепловых процессов, теории упругости и др.

Мы же воспользуемся довольно простыми методами исследования, но которые, как подтверждает практика, достаточно правильно объясняют явление удара.

Поскольку сила удара   очень велика, а продолжительность его, время  , мало,  при описании процесса удара будем пользоваться не дифференциальными уравнениями движения, а теоремой об изменении количества движения. Потому что измеряемой конечной величиной является не сила удара, а импульс ее 

Чтобы сформулировать первые особенности явления удара, рассмотрим сначала действие такой силы на материальную точку.

Пусть к материальной точке М, движущейся под действием обычных сил   по некоторой траектории (рис.111), в какой-то момент была приложена  мгновенная,  большая  сила  . С помощью теоремы об изменении количества движения за время удара   составляем уравнение   где   и   - скорости точки в конце и в начале удара;   - импульс мгновенной силы  . Импульсами обычных сил, под действием которых точка двигалась, можно пренебречь – за время   они будут очень малы.

Рис.111

 

Из  уравнения  находим  изменение   скорости  за  время  удара (рис.111):

.

Это изменение скорости оказывается конечной величиной.

Дальнейшее движение точки начнется со скоростью   и продолжится под действием прежних сил, но по траектории, получившей излом.

Теперь можно сделать несколько выводов.

1. При  исследовании  явления  удара  обычные силы можно не учитывать.

2. Так как время   мало, перемещением точки за время удара можно пренебречь.

3. Единственный результат действия удара – только изменение вектора скорости.

Взаимодействие тел, при котором за малый промежуток времени  скорости точек изменяются на конечную величину, называется ударом. Время удара  измеряется сотыми, тысячными и менее долями секунды. Силы, возникающие при таком взаимодействии, называются ударными.

Прямым центральным ударом называют такое взаимодействие тел, при котором их скорости направлены по общей нормали в точке касания, и эта точка лежит на прямой, соединяющей центры масс.

На Рис. 3.9.1 показано изменение скорости   при ударе материальной точки о неподвижную преграду. Здесь   – скорость в момент начала удара,   – скорость при окончании удара. При прямом ударе

,

а при косом

.

При расчетах в элементарной теории удара принимают следующие допущения:

1) скорости точек изменяются скачкообразно;

2) импульсы обычных сил малы по сравнению с импульсами ударных сил;

3) перемещениями точек за время удара можно пренебречь.

Физические свойства соударяющихся тел характеризуются коэффициентом восстановления

                                            (3.9.1)

являющимся отношением проекций относительной скорости точки контакта тел после удара и до удара на направление общей нормали к поверхно­стям тел в точке соприкосновения (гипотеза Ньютона). Коэффициент восстановления определяется экспериментально и его значения имеются в справочной литературе. При ударе материальной точки о неподвижную поверхность (Рис. 3.9.1) коэффициент восстановления будет

  или 

Основное уравнение теории удара. Изменение количества движения материальной точки за время удара равно сумме ударных импульсов, действующих на точку

,                                   (3.9.2)

где   – скорость материальной точки до удара,   – скорость этой точки после удара,   – импульс ударных сил.

Теорема об изменении количества движения механической системы при ударе. Изменение количества движения механической системы за время удара равно сумме внешних ударных  импульсов, действующих на точки системы:

.

Теорема об изменении кинетического момента механической системы при ударе. Изменение кинетического момента механической системы относительно любого неподвижного центра (оси) за время удара равно сумме моментов всех внешних ударных импульсов, приложенных к точкам системы, относительно этого же центра (оси):

,     .

Теорема о потере кинетической энергии (теорема Карно). При неупругом ударе в механической системе потеря кинетической энергии равна кинетической энергии данной системы, если бы она двигалась с потерянными скоростями

.

В случае упругого удара:

.

Определение импульсов ударных реакций при ударе по вращающемуся телу

Пусть   – ударный импульс, приложенный в некоторой точке тела (Рис. 3.9.1). Проведем координатную плоскость, например Oyz, через центр масс тела (через точку С), совместив ось Oz с осью вращения.

Запишем теоремы об изменении количества движения и кинетического момента механической системы для удара в проекциях на оси координат

,

,

,                                             (3.9.3)

,

,

.

Из этих уравнений находим ударные реакции и угловую скорость после удара.

Центр удара – это точка вращающегося тела, при действии на которую ударного импульса не возникает ударной реакции.

Для того, чтобы при действии ударного импульса на вращающееся тело в подшипниках не возникали ударные реакции, нужно, чтобы выполнялись следующие условия.

1. Точка приложения ударного импульса должна лежать в плоскости, проходящей через центр масс и ось вращения, на расстоянии  .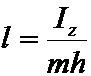

2. Ударный импульс должен быть направлен перпендикулярно этой плоскости.

3. Ось вращения должна являться главной для точки её пересечения с плоскостью действия ударного импульса.

Теорема об изменении количества движения.

Рассмот­рим систему, состоящую из п материальных точек. Составим для этой системы дифференциальные уравнения движения  и сложим их почленно. Тогда получим:

.

Последняя сумма по свойству внутренних сил равна нулю. Кроме того,                  

Окончательно находим:

.

Уравнение выражает теорему об изменении коли­чества  движения  системы  в  дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил. В проекциях на координатные оси будем иметь:

         

Найдем другое выражение теоремы. Пусть в момент   количество движения системы равно  , а в момент   становится равным  . Тогда, умножая обе части равенства   на dt и интегрируя, получим:

или

так как интегралы, стоящие справа, дают импульсы внешних сил.

Уравнение выражает теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за некоторый промежу­ток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени.

В проекциях на координатные оси будем иметь:

       

Укажем на связь между доказанной теоремой и теоремой о дви­жении центра масс. Так как   то, подставляя это значение в равенство и учитывая, что  , мы получим  .

Следовательно, теорема о движении центра масс и теорема об изменении количества движения системы представляют собой, по существу, две разные формы одной и той же теоремы. В тех случаях, когда изучается движение твердого тела (или системы тел), можно в равной мере пользоваться любой из этих форм.

Практическая ценность теоремы состоит в том, что она позволяет исключить из рассмотрения наперед неизвестные внутренние силы (например, силы давления друг на друга частиц жидкости).

УДАР   ТЕЛА   О   НЕПОДВИЖНУЮ   ПРЕГРАДУ

Рассмотрим  тело  (шар) массой M , ударяющееся  о   неподвижную  плиту.

Действующей на  тело  ударной силой будет при этом реакция плиты; импульс

этой силы за время  удара  назовем

S. Пусть нормаль к поверхности тела в

точке его касания с плитой проходит через центр масс тела (для шара это

будет всегда). Такой удар тела называется центральным. Если скорость v

центра масс тела в начале удара направлена по нормали n к плите, то удар

будет прямым, в противном случае -- косым.

. Случаи прямого удара.

Составляя в этом случае уравнение (154) в

проекции на нормаль n (см. рис. 375) и учитывая, что Q0 = M v, a Q0 = M u,

получим

M (un - vn) = Sn.

Но при прямом ударе un = u, vn = -v, Sn = S. Следовательно,

M (u + v) = S.

Второе уравнение, необходимое для решения задачи, дает равенство

u = kv.

Из полученных уравнений, зная M , v, k, найдем неизвестные величины u и

S. При этом

S = M (1 + k)v.

Как видим, ударный импульс будет тем больше, чем больше коэффициент

восстановления k. На эту зависимость S от k и было указано в 153.

Чтобы определить среднюю величину ударной силы (реакции), надо до-

полнительно знать время удара , которое можно найти экспериментально.

Пример

. При падении стального шара массой m = 1 кг с высоты H = 3

м на стальную плиту (k = 0, 56) получим v = √2gH ≈ 7,7м/с и u = kv = 4,3

м/с. Ударный импульс S = mv(1 + k) ≈ 12Нс. Если время удара = 0,0005c,

то средняя величина ударной реакции N

уд

ср = S/ = 24000Н.

2. Случаи косого удара.

Пусть в этом случае скорость v центра масс

тела в начале удара образует с нормалью к плите угол , а скорость u в

конце удара -- угол (рис. 377)

Тогда уравнение (154) в проекциях на касательную и нормаль n даст

M (u - v) = 0, M(un - vn) = S.

Коэффициент восстановления в данном случае равен отношению: модулей

|un| и |vn|, так как удар происходит только по направлению нормали к по-

верхности (влиянием трения пренебрегаем). Тогда с учетом знаков проекций

получим un = -kvn. В результате окончательно находим:

u = v , un =

-kvn, S = M|vn|(1 + k).

Из полученных уравнений можно найти модуль и направление скорости в

конце удара и ударный импульс, если величины M , V , , и k известны. В

частности, из первого равенства, замечая, что v = |vn|tg и u = |un|tg,

получаем

|un|tg = |vn|tg ,

откуда

k = |un|/|vn| = tg / tg .

Следовательно, при косом ударе отношение тангенса угла падения, к тан-

генсу угла отражения равно коэффициенту восстановления. Так как k < 1,

то < , т. е, угол падения всегда меньше угла отражения

Удар абсолютно упругих и неупругих тел

Примером применения законов сохранения импульса и энергии при решении реальной физической задачи является удар абсолютно упругих и неупругих тел.

Удар (или соударение)—это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. Помимо ударов в прямом смысле этого слова (столкновения атомов или биллиардных шаров) сюда можно отнести и такие, как удар человека о землю при прыжке с трамвая и т. д. Силы взаимодействия между сталкивающимися телами (ударные или мгновенные силы) столь велики, что внешними силами, действующими на них, можно пренебречь. Это позволяет систему тел в процес­се их соударения приближенно рассматривать как замкнутую систему и применять к ней законы сохранения.

Тела во время удара претерпевают деформацию. Сущность удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами. Наблюдения пока­зывают, что относительная скорость тел после удара не достигает своего прежнего значения. Это объясняется тем, что нет идеально упругих тел и идеально гладких поверхностей. Отношение нормальных составляющих относительной скорости тел после и да удара называется коэффициентом восстановления :

Если для сталкивающихся тел =0, то такие тела называются абсолютно неупругими, если =1 — абсолютно упругими. На практике для всех тел 0 <  < 1 (например, для стальных шаров 0,56, для шаров из слоновой кости 0,89, для свинца 0). Однако в некоторых случаях тела можно с большой степенью точности рассматривать либо какабсолютно упругие, либо как абсолютно неупругие.

Прямая, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения, называется линией удара. Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через их центры масс. Мы будем рассматривать только центральные абсолютно упругие и абсолютно неупругие удары.

Абсолютно упругий удар — столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энер­гия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию (подчеркнем, что это идеализированный случай).

Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения кинетической энергии.

Обозначим скорости шаров массами т₁ и m₂ до удара через v₁ и v₂, после удара—через   и   (рис. 18). В случае прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, соединяющей их центры. Проекции векторов скорости на эту линию равны модулям скоростей. Их направления учтем знаками: положительное значение припишем движению вправо, отрицатель-нос — движению влево.

При указанных допущениях законы сохранения имеют вид

                                                              (15.1)

                                                              (15.2)

Произведя соответствующие преобразования в выражениях (15.1) и (15.2), получим

                                                                (15.3)

                                                              (15.4)

откуда

                                                                             (15.5)

Решая уравнения (15.3) и (15.5), находим

                                                       (15.6)

                                                      (15.7)

Разберем несколько примеров.

1. При v₂=0

                                                                    (15.8)

                                                                     (15.9)

Проанализируем выражения (15.8) в (15.9) для двух шаров различных масс:

а) т₁=т₂. Если второй шар до удара висел неподвижно (v₂=0) (рис. 19), то после удара остановится первый шар ( =0), а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался первый шар до удара ( );

б) т₁>т₂. Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью ( <v₁). Скорость второго шара после удара больше, чем скорость первого после удара ( > ) (рис. 20);

в) т₁<т₂. Направление движения первого шара при ударе изменяется—шар отскакивает обратно. Второй шар движется в ту же сторону, в которую двигался первый шар до удара, но с меньшей скоростью, т. е.  <v₁ (рис. 21);

г) т₂>>т₁ (например, столкновение шара со стеной). Из уравнений (15.8) и (15.9) следует, что   = –v₁,  2m₁v₁/m₂0.

2. При т₁=т₂ выражения (15.6) и (15.7) будут иметь вид

т. е. шары равной массы «обмениваются» скоростями.

Абсолютно неупругий удар — столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. Продемонстрировать абсолютно неупругий удар можно с помощью шаров из пластилина (глины), движущихся навстре­чу друг другу (рис. 22).

Если массы шаров т₁ и т₂, их скорости до удара v₁ и v₂, то, используя закон сохранения импульса, можно записать

где v — скорость движения шаров после удара. Тогда

                                                          (15.10)

Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим импульсом. В частном случае, если массы шаров равны (т₁=т₂), то

Выясним, как изменяется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения шаров между ними действуют силы, зависящие не от самих деформаций, а от их скоростей, то мы имеем дело с силами, подобными силам трения, поэтому закон сохранения механической энергии не должен соблюдаться. Вследствие деформации происходит «потеря» кинетической энергии, перешедшей в тепловую или другие формы энергии. Эту «потерю» можно определить по разности кинетической энергии тел до и после удара:

Используя (15.10), получаем

   

Если ударяемое тело было первоначально неподвижно (v₂=0), то

Когда m₂>>m₁ (масса неподвижного тела очень большая), то v<<v₁ и почти вся кинети­ческая энергия тела при ударе переходит в другие формы энергии. Поэтому, например, для получения значительной деформации наковальня должна быть массивнее молотка. Наоборот, при забивании гвоздей в стену масса молотка должна быть гораздо большей (m₁>>m₂),тогда vv₁ и практически вся энергия затрачивается на возможно большее перемещение гвоздя, а не на остаточную деформацию стены.

Абсолютно неупругий удар — пример того, как происходит «потеря» механической энергии под действием диссипативных сил.

1.21. Упругие и неупругие соударения

Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.

Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.

С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).

В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).

Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью   попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.

Обозначим скорость ящика с застрявшей в нем пулей через   Тогда по закону сохранения импульса 

При застревании пули в песке произошла потеря механической энергии: 

Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы: 

Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.

При m << M 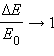  почти вся кинетическая энергия пули переходит во внутреннюю энергию. При m = M 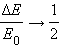  – во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m >> М) отношение 

Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии: 

где h – максимальная высота подъема маятника. Из этих соотношений следует: 

Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.

Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.

Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.

В общем случае массы m₁ и m₂ соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии 

Здесь υ₁ – скорость первого шара до столкновения, скорость второго шара υ₂ = 0, u₁ и u₂ – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде: 

m1υ1 = m1u1 + m2u2.

Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u₁ и u₂ шаров после столкновения: 

В частном случае, когда оба шара имеют одинаковые массы (m₁ = m₂), первый шар после соударения останавливается (u₁ = 0), а второй движется со скоростью u₂ = υ₁, т. е. шары обмениваются скоростями (и, следовательно, импульсами).

Если бы до соударения второй шар также имел ненулевую скорость (υ₂ ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ₂ относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ₁' = υ₁ – υ₂. Определив по приведенным выше формулам скорости u₁ и u₂шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.

Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.

Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.

Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).

После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей   и   после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости   налетающего шара. Если массы шаров одинаковы, то векторы скоростей   и   шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m₁ = m₂ = m эти законы принимают вид: 

Первое из этих равенств означает, что векторы скоростей  ,   и   образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами  и   равен 90°.

“Потеря  кинетической  энергии  тел  при  неупругом  ударе  равна   кинетической энергии  этих  тел, рассчитанной  по  потерянным скоростям”.

         Доказательство  этой  теоремы для самого простого случая  -  удара  тела  о гладкую  поверхность приведено выше.    Очень длинное доказательство  этой  же  теоремы  для случая соударения двух движущихся до и после удара  тел  приведено  в  [5]. 

         Рассматривая далее при тех же допущениях  ударные  явления  в  системе  материальных  точек  можно  доказать:

         1. Изменение количества движения  механической  системы  при  ударных  явлениях  определяется  импульсами  только  внешних ударных  сил.

         2. Изменение  момента  количества  движения  механической системы относительно  некоторого  центра  при  ударе  равно  геометрической  сумме  моментов  импульсов  внешних  ударных  сил.

         ( Ранее  теорема  об  изменении  кинетического  момента  механической  системы  записывалась  только в  дифференциальной форме. )

 

               Доказательства  теорем,  выводы  из  них,  некоторые  примеры  решения  задач  более  подробно  даны  в других  учебниках.

 

Закончим же краткий экскурс в теорию удара вопросами приближенной  оценки  ударных сил  и получения желаемого эффекта при ударе одного тела  по  другому.

 

Исследования показывают,  что примерный график изменения величины ударной силы за время удара имеет вид, приведенный  на  рисунке.

 

 

Для приближенной оценки  величины ударной  силы  кроме  ударного  импульса,  определяемого  по “потерянной  скорости”,  необходимо  знать  и  время  удара.

         Среднее  значение  ударной  силы можно  определить,  разделив  величину ударного импульса  на  время удара.   Максимальное значение  ударной  силы примерно  на  50 %  больше.

 

Для  получения желаемого  эффекта при ударе одного тела по другому  целесообразно  знать решение  следующей  задачи. 

         Пусть  тело  массой   m₁  со  скоростью  V   ударяется  о  неподвижное  до  удара тело массой  m₂ .  Удар  абсолютно неупругий.  Найдем для разных  соотношений  масс  соударяющихся  тел  их скорость после удара  и  потерю  кинетической  энергии  в  каждом  из  случаев.

         После  неупругого  удара  движущегося тела о неподвижное оба тела  начнут  двигаться  со  скоростью,  которую  можно  определить  на  основании  закона  сохранения  количества движения  системы  тел.  

Из  конечного  выражения  следует :

         1.   При   m₁  >>  m₂    T   0.   Следовательно,  несмотря  на  то,  что  удар  является  неупругим,  потери  кинетической  энергии  при  ударе  не  происходит.  Бывшее  неподвижным  тело после удара начинает  двигаться с кинетической  энергией,  равной  кинетической  энергии  первого  тела  до удара.   Это важно  знать  при  расчете  массы  копра  для  забивки  свай,  при  подборе  массы  молота в  зависимости от  забиваемых  гвоздей  и во  всех  случаях,  когда  с  помощью  удара  необходимо  привести  в  движение  другое  тело.

         2.   При   m₁  << m₂    T    T₀.    В  этом  случае  кинетическая  энергия  практически  полностью  расходуется  на  деформацию  соударяющихся  тел.  Это важно знать при выборе соотношения между  массой  молота,  детали  и наковальни,  на  которой обрабатывается  деталь.  Масса  наковальни  должна  быть  во  много  раз  больше  массы  молота.  То же  касается  и выбора поддерживающей  детали  при  клепке.