
- •2.Определители, их свойства.
- •3. Минор, алгебраическое дополнение. Вычисления определителей с помощью алгебраических дополнений (т.Лапласа)
- •4.Формула Крамера для решения систем линейных уравнений. (слу)
- •5. Решение однородных систем линейных уравнений.
- •6.Обратная матрица, матричная форма записи слу, решение слу с помощью обратной матрицы.
- •7.Метод Гаусса для решения слу (общий случай система n-го порядка)
- •8.Ранг матрицы, теорема Кронекера-Капелли.
- •9.Понятие вектора, проекция вектора на оси координат, направляющие косинусы.
- •10.Линейные операции над векторами, их основные свойства, колинеарность, компланарность векторов.
- •11.Разложение вектора по базису
- •12.Скалярное произведение векторов, их свойства
- •13. Векторное произведение векторов, их свойства.
- •14. Смешанное произведение векторов, его свойства.
- •15.Расстояние между двумя точками на плоскости. Нахождение площади треугольника, деление отрезка в заданном отношении.
- •16.Уравнение прямой на плоскости: с угловым коэффициентом; проходящей через данную точку с угловым коэффициентом; проходящей через две данные точки.
- •17.Угол между двумя прямыми, условия параллельности и перпендикулярности прямых на плоскости.
- •18.Общее уравнение прямой , нормально уравнение прямой, расстояние от точки до прямой.
- •19.Приведение общего уравнения прямой к нормальному виду, нормирующий множитель. (пример)
- •20.Понятие о линиях второго порядка: эллипс, гипербола, парабола. Общее уравнение линии второго порядка.
- •Угол между плоскостями.
- •25.Расстояние от точки до прямой в пространстве. Взаимное расположение прямой и плоскости.
- •26.Предел функции непрерывного аргумента (примеры). Бесконечно большой аргумент.
- •27.Предел числовой последовательности (пример).
- •28.Бесконечно большие, ограниченные, бесконечно малые функции (примеры)
- •29.Сравнение бесконечно малых функций, эквивалентные бесконечно малые.
- •30.Таблица эквивалентов (доказательство.
- •31.Правила предельного перехода: предел суммы, произведения, частного функции (доказательство)
- •32.Признак существования предела функции. Первый замечательный предел(доказательство)
- •33.Признак существования предела числовой последовательности. Второй замечательный закон.
- •34.Непрерывность функций, классификация точек разрыва (пример)
- •35.Действия над непрерывными функциями. Свойства непрерывных функций.
- •36.Понятие производной функции, геометрический смысл (пример)
- •37.Необходимое условие существования производной (пример)
- •38.Теоремы о производных суммы, произведения, частного функций (доказательство)
- •39.Производная сложной функции, производная неявной функции, производная обратной функции.
- •40.Логарифмическая производная. Дифференцирование функций, заданных параметрически (примеры)
- •41.Таблица производных элементарных функций (доказательство)
- •42.Дифференцируемость функций, необходимое и достаточное условия дифференцируемости функций.
- •43.Дифференциал функции, дифференциал суммы, производная, частного, применение дифференциала в приближенных вычислениях.
- •44.Производные и дифференциалы высших порядков.
- •49.Формула Тейлора, формула Маклорена, разложение некоторых элементарных функций по формуле Маклорена.
- •50.Возрастание и убывание функций. Необходимое и достаточное условие монотонности функций. Экстремальные точки. Достаточные условия экстремума (примеры)
- •51.Выпуклость и вогнутость кривой. Достаточные условия точек перегиба (пример)
- •52.Асимптоты графиков функций (примеры)
- •53.Исследование функций, построение их графиков (примеры)
15.Расстояние между двумя точками на плоскости. Нахождение площади треугольника, деление отрезка в заданном отношении.
Расстояние между двумя точками ( х1 , у 1 , z 1 ) и ( x2 , y2 , z2) :
![]()
Расстояние от точки ( х0 , у 0 , z 0 ) до плоскости Ах + Ву + Сz + D = 0 :
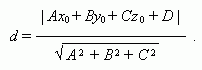
ha - высота, проведенная к стороне a.
p - полупериметр, т.е. половина от суммы всех сторон треугольника.
R - радиус описанной окружности.
r - радиус вписанной окружности.
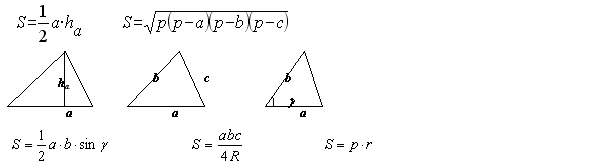
16.Уравнение прямой на плоскости: с угловым коэффициентом; проходящей через данную точку с угловым коэффициентом; проходящей через две данные точки.
В
декартовой системе координат на
плоскости общее уравнение прямой имеет
вид
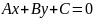 .
Уравнение прямой с угловым коэффициентом
.
Уравнение прямой с угловым коэффициентом
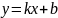 ,
,
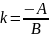 ,
,
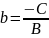 .
Уравнение прямой, проходящей через
данную точку и имеющей угловой коэффициент
.
Уравнение прямой, проходящей через
данную точку и имеющей угловой коэффициент
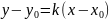 .
Уравнение прямой, проходящей через две
заданные точки
.
Уравнение прямой, проходящей через две
заданные точки
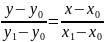
17.Угол между двумя прямыми, условия параллельности и перпендикулярности прямых на плоскости.
Угол между прямыми. Угол между прямой и плоскостью
Определение. Углом между прямыми в пространстве называют любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Угол
между прямыми в пространстве равен
углу между их направляющими векторами ![]() .
Поэтому, если две прямые заданы
каноническими уравнениями вида
.
Поэтому, если две прямые заданы
каноническими уравнениями вида ![]() и
и ![]() то
косинус угла между ними можно найти по
формуле:
то
косинус угла между ними можно найти по
формуле:
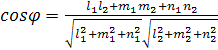 ).
).
Пример.
Найти угол между прямыми ![]() и
и ![]() .
.
Решение.
По условию ![]() ,
тогда
,
тогда
отсюда
![]()
![]() ,
, ![]() ,
, ![]() .
.
Условия параллельности и перпендикулярности прямых
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов .
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны:
![]() –
условие
параллельности прямых.
–
условие
параллельности прямых.
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:
![]() –
условие
перпендикулярности прямых.
–
условие
перпендикулярности прямых.
18.Общее уравнение прямой , нормально уравнение прямой, расстояние от точки до прямой.
В
декартовой системе координат на
плоскости общее уравнение прямой имеет
вид
.
Нормальное уравнение прямой
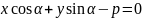 .
Расстояние от точки до прямой, заданной
а)общим
уравнением
.
Расстояние от точки до прямой, заданной
а)общим
уравнением
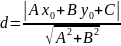 ;
б)нормальным
уравнением
;
б)нормальным
уравнением
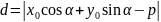
19.Приведение общего уравнения прямой к нормальному виду, нормирующий множитель. (пример)
Очень часто в условиях задач, решение которых подразумевает использование нормального уравнения прямой, уравнение прямой линии дается не в нормальном виде, а в каком-либо другом. Поэтому встает новая задача: привести заданное уравнение прямой к нормальному виду. Сейчас мы с ней и разберемся.
Сразу отметим, что нормальное уравнение прямой можно получить из общего уравнения прямой. Если прямая на плоскости задана иным уравнением прямой, то это уравнение следует сначала привести к общему уравнению прямой, а уже после этого приводить общее уравнение прямой к нормальному виду.
Итак,
покажем приведение общего уравнения
прямой ![]() к
нормальному уравнению прямой.
к
нормальному уравнению прямой.
Чтобы
привести общее уравнение прямой к
нормальному виду нужно обе части
равенства
умножить
на так называемый нормирующий
множитель,
который равен  .
Знак нормирующего множителя берется
противоположным знаку слагаемого С.
Если C = 0,
то знак нормирующего множителя не имеет
значения и может быть выбран произвольно.
.
Знак нормирующего множителя берется
противоположным знаку слагаемого С.
Если C = 0,
то знак нормирующего множителя не имеет
значения и может быть выбран произвольно.
Рассмотрим решения нескольких примеров.
Пример.
Приведите
уравнение прямой ![]() к
нормальному виду.
к
нормальному виду.
Решение.
Нам
дано общее уравнение прямой, в
котором А = 3, В = -4, С = -16.
Таким образом, нормирующий множитель
следует брать со знаком «+», так как С –
отрицательное число. Вычислим значение
нормирующего множителя: ![]() .
Умножаем на одну пятую обе части
исходного уравнения:
.
Умножаем на одну пятую обе части
исходного уравнения: ![]() .
Последнее равенство является нормальным
уравнением заданной прямой.
.
Последнее равенство является нормальным
уравнением заданной прямой.
Ответ:
![]()
