
- •2.Определители, их свойства.
- •3. Минор, алгебраическое дополнение. Вычисления определителей с помощью алгебраических дополнений (т.Лапласа)
- •4.Формула Крамера для решения систем линейных уравнений. (слу)
- •5. Решение однородных систем линейных уравнений.
- •6.Обратная матрица, матричная форма записи слу, решение слу с помощью обратной матрицы.
- •7.Метод Гаусса для решения слу (общий случай система n-го порядка)
- •8.Ранг матрицы, теорема Кронекера-Капелли.
- •9.Понятие вектора, проекция вектора на оси координат, направляющие косинусы.
- •10.Линейные операции над векторами, их основные свойства, колинеарность, компланарность векторов.
- •11.Разложение вектора по базису
- •12.Скалярное произведение векторов, их свойства
- •13. Векторное произведение векторов, их свойства.
- •14. Смешанное произведение векторов, его свойства.
- •15.Расстояние между двумя точками на плоскости. Нахождение площади треугольника, деление отрезка в заданном отношении.
- •16.Уравнение прямой на плоскости: с угловым коэффициентом; проходящей через данную точку с угловым коэффициентом; проходящей через две данные точки.
- •17.Угол между двумя прямыми, условия параллельности и перпендикулярности прямых на плоскости.
- •18.Общее уравнение прямой , нормально уравнение прямой, расстояние от точки до прямой.
- •19.Приведение общего уравнения прямой к нормальному виду, нормирующий множитель. (пример)
- •20.Понятие о линиях второго порядка: эллипс, гипербола, парабола. Общее уравнение линии второго порядка.
- •Угол между плоскостями.
- •25.Расстояние от точки до прямой в пространстве. Взаимное расположение прямой и плоскости.
- •26.Предел функции непрерывного аргумента (примеры). Бесконечно большой аргумент.
- •27.Предел числовой последовательности (пример).
- •28.Бесконечно большие, ограниченные, бесконечно малые функции (примеры)
- •29.Сравнение бесконечно малых функций, эквивалентные бесконечно малые.
- •30.Таблица эквивалентов (доказательство.
- •31.Правила предельного перехода: предел суммы, произведения, частного функции (доказательство)
- •32.Признак существования предела функции. Первый замечательный предел(доказательство)
- •33.Признак существования предела числовой последовательности. Второй замечательный закон.
- •34.Непрерывность функций, классификация точек разрыва (пример)
- •35.Действия над непрерывными функциями. Свойства непрерывных функций.
- •36.Понятие производной функции, геометрический смысл (пример)
- •37.Необходимое условие существования производной (пример)
- •38.Теоремы о производных суммы, произведения, частного функций (доказательство)
- •39.Производная сложной функции, производная неявной функции, производная обратной функции.
- •40.Логарифмическая производная. Дифференцирование функций, заданных параметрически (примеры)
- •41.Таблица производных элементарных функций (доказательство)
- •42.Дифференцируемость функций, необходимое и достаточное условия дифференцируемости функций.
- •43.Дифференциал функции, дифференциал суммы, производная, частного, применение дифференциала в приближенных вычислениях.
- •44.Производные и дифференциалы высших порядков.
- •49.Формула Тейлора, формула Маклорена, разложение некоторых элементарных функций по формуле Маклорена.
- •50.Возрастание и убывание функций. Необходимое и достаточное условие монотонности функций. Экстремальные точки. Достаточные условия экстремума (примеры)
- •51.Выпуклость и вогнутость кривой. Достаточные условия точек перегиба (пример)
- •52.Асимптоты графиков функций (примеры)
- •53.Исследование функций, построение их графиков (примеры)
9.Понятие вектора, проекция вектора на оси координат, направляющие косинусы.
Вектором называется
направленный отрезок, имеющий определенную
длину, т. е. отрезок определенной длины,
у которого одна из ограничивающих
его точек принимается за начало, а
вторая — за конец
Проекцией вектора
на ось называется вектор, который
получается в результате перемножения
скалярной проекции вектора на эту ось
и единичного вектора этой оси. Например,
если аx – скалярная
проекция вектора а на
ось X, то аx·i -
его векторная проекция на эту
ось.
Обозначим векторную
проекцию также,
как и сам вектор, но с индексом той оси
на которую вектор проектируется. Так,
векторную проекцию вектора а на
ось Х обозначим аx (жирная буква,
обозначающая вектор и нижний индекс
названия оси) или ![]() (нежирная
буква, обозначающая вектор, но со
стрелкой
наверху
(!) и нижний индекс названия
оси).
(нежирная
буква, обозначающая вектор, но со
стрелкой
наверху
(!) и нижний индекс названия
оси).
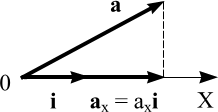 Скалярной
проекцией вектора
на ось называется число,
абсолютная величина которого равна
длине отрезка оси (в выбранном масштабе),
заключённого между проекциями точки
начала и точки конца вектора. Обычно
вместо выражения скалярная
проекция говорят
просто – проекция.
Проекция обозначается той же буквой,
что и проектируемый вектор (в обычном,
нежирном написании), с нижним (как
правило) индексом названия оси, на
которую этот вектор проектируется.
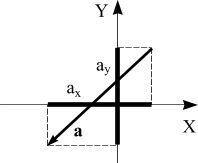
Например, если на ось Х проектируется
вектора, то
его проекция обозначается аx.
При проектировании этого же вектора
на другую ось, если ось
Y , его проекция будет обозначаться
аy .
Скалярной
проекцией вектора
на ось называется число,
абсолютная величина которого равна
длине отрезка оси (в выбранном масштабе),
заключённого между проекциями точки
начала и точки конца вектора. Обычно
вместо выражения скалярная
проекция говорят
просто – проекция.
Проекция обозначается той же буквой,
что и проектируемый вектор (в обычном,
нежирном написании), с нижним (как
правило) индексом названия оси, на
которую этот вектор проектируется.
Например, если на ось Х проектируется
вектора, то
его проекция обозначается аx.
При проектировании этого же вектора
на другую ось, если ось
Y , его проекция будет обозначаться
аy .
 Чтобы
вычислить проекцию вектора на
ось (например, ось X) надо из координаты
точки его конца вычесть координату
точки начала, то есть
аx =
хк −
xн.
Проекция
вектора на ось - это число. Причем,
проекция может быть положительной,
если величина хк больше
величины хн,
отрицательной, если
величина хк меньше
величины хн
и
равной нулю, если хк равно
хн .
Чтобы
вычислить проекцию вектора на
ось (например, ось X) надо из координаты
точки его конца вычесть координату
точки начала, то есть
аx =
хк −
xн.
Проекция
вектора на ось - это число. Причем,
проекция может быть положительной,
если величина хк больше
величины хн,
отрицательной, если
величина хк меньше
величины хн
и
равной нулю, если хк равно
хн .
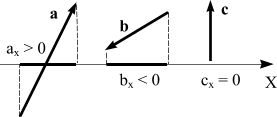 Проекцию
вектора на ось можно также найти, зная
модуль вектора и угол, который он
составляет с этой осью.
Из
рисунка видно,
что аx =
а Cos α
то есть, проекция вектора
на ось равна произведению модуля вектора
на косинус угла между направлением оси
и направлением
вектора.
Если угол острый, то
Cos α > 0 и
аx >
0, а, если тупой, то косинус тупого угла
отрицателен, и проекция вектора на ось
тоже будет отрицательна.
Проекцию
вектора на ось можно также найти, зная
модуль вектора и угол, который он
составляет с этой осью.
Из
рисунка видно,
что аx =
а Cos α
то есть, проекция вектора
на ось равна произведению модуля вектора
на косинус угла между направлением оси
и направлением
вектора.
Если угол острый, то
Cos α > 0 и
аx >
0, а, если тупой, то косинус тупого угла
отрицателен, и проекция вектора на ось
тоже будет отрицательна.
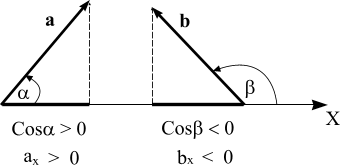 Углы,
отсчитываемые от оси против хода часовой
стрелки, принято считать положительными,
а по ходу - отрицательными. Однако,
поскольку косинус – функция четная,
то есть, Cos α = Cos (− α), то при вычислении
проекций углы можно отсчитывать как
по ходу часовой стрелки, так и
против.
Чтобы
найти проекцию вектора на ось надо
модуль этого вектора умножить на косинус
угла между направлением оси и направлением
вектора.
Углы,
отсчитываемые от оси против хода часовой
стрелки, принято считать положительными,
а по ходу - отрицательными. Однако,
поскольку косинус – функция четная,
то есть, Cos α = Cos (− α), то при вычислении
проекций углы можно отсчитывать как
по ходу часовой стрелки, так и
против.
Чтобы
найти проекцию вектора на ось надо
модуль этого вектора умножить на косинус
угла между направлением оси и направлением
вектора.
10.Линейные операции над векторами, их основные свойства, колинеарность, компланарность векторов.
Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.Замечание. Такое правило сложения векторов называют правилом треугольника.
Свойства сложения:
Свойство 1. a + b = b + a
Свойство 2. (a+b)+c=a+(b+c).
Свойство 3. Для любого вектора a существует нулевой вектор О такой, что a+О=а.
Свойство 4. Для каждого вектора a существует противоположный ему вектор a/ такой, что а+а/=О.
Доказательство. Достаточно определить a/ как вектор, коллинеарный вектору a, имеющий одинаковую с ним длину и противоположное направление.
Разностью а – b векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.
Произведением ka вектора а на число k называется вектор b, коллинеарный вектору а, имеющий модуль, равный |k||a|, и направление, совпадающее с направлением а при k>0 и противоположное а при k<0.
Свойства умножения вектора на число:
Свойство 1. k(a + b) = ka + kb.
Свойство 2. (k + m)a = ka + ma.
Свойство 3. k(ma) = (km)a.
Следствие. Если ненулевые векторы а и b коллинеарны, то существует такое число k, что b = ka.
Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости
