1.Матрица, виды матриц. Действия над матрицами. Матрица – прямоугольная таблица чисел или функций 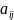, где 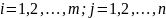, состоящая из строк и столбцов.Виды матриц: Диагональная матрица – квадратная матрица, все элементы которой , стоящие на главной диагонали, отличны от нуля, а все остальные элементы равны нулю. Единичная матрица – диагональная матрица. Все диагональные элементы которой равны единицам (Е) Нулевая матрица – матрица, у которой все элементы равны нулю. (О) Действия над матрицами: Равенство матриц – две матрицы считаются равными, если эти матрицы имеют одинаковые размеры и все их соответствующие элементы совпадают. Сумма матриц – суммой двух матриц одинаковых размеров называется матрица тех же размеров, элементы которой равны сумме соответствующих элементов матриц-слагаемых. Произведение матрицы на число– произведением матрицы на вещественное число называется матрица тех же размеров , элементы которой равны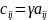 Транспонирование матрицы – матрица В называется транспонированной по отношению к матрице А, если строки матрицы А превращаются в столбцы матрицы В с сохранением порядка их следования. Произведение матриц – произведение матрицы А размером (m,k) на матрицу В размером (k,n) называется матрица С=АВ размером (m,n)=(m,k)(k,n)

2.Определители, их свойства.

Определитель порядка n, соответствующий матрице А – число, обозначаемое detA и вычисляемое по формуле 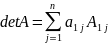, где А – алгебраическое дополнение. Свойства определителей: 1.Строки и столбцы определителя равны, т.е. величина определителя не изменится, если поменять местами его строки и столбцы с сохранением порядка их следования. (транспонирование) 2.При перестановке местами двух строк (столбцов) определители сохраняют свою абсолютную величину, но меняют знак на противоположный. 3.Определитель с двумя одинаковыми строками (столбцами) равен нулю. 4.Умножение всех элементов некоторой строки (столбца) определителя на число равносильно умножению определителя на число. 5.Если все элементы какой-либо строки (столбца) определителя равны нулю, то и сам определитель равен нулю. 6.Если элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю. 7.Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель, то величина определителя не изменится. 8.Сумма произведений элементов какой-либо строки (столбца) определителя на соответствующие алгебраические дополнения элементов любой другой строки (столбца) равно нулю. 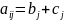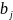9.Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых , то определитель равен сумме двух определителей, у которых все строки, кроме i-й,такие же, как и в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов , а в другом – из элементов 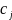10.Определитель произведения двух квадратных матриц равен произведению их определителей.

3. Минор, алгебраическое дополнение. Вычисления определителей с помощью алгебраических дополнений (т.Лапласа)

Минор – определитель n-1-го порядка, соответствующий той матрице, которая получается из матрицы А в результате вычеркивания i-й строки и J-го столбца, на пересечении которых стоит элемент . Минор для элемента матрицы первого порядка, состоящей всего из одного элемента, равен этому элементу. Алгебраическое дополнение – минор 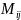этого элемента, взятый со знаком «+», если сумма индексов строки и столбца (i+j), на пересечении которых стоит этот элемент, четная, и со знаком «-«, если сумма индексов нечетная. Теорема Лапласа Пусть выбраны любы  строк матрицы . Тогда определитель матрицы  равен сумме всевозможных произведений миноров -го порядка, расположенных в этих строках, на их алгебраические дополнения. где суммирование ведётся по всевозможным номерам столбцов 

4.Формула Крамера для решения систем линейных уравнений. (слу)

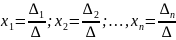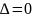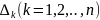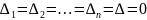1.Если определитель основной матрицы квадратной системы отличен от нуля, со система имеет единственное решение, которое определяется формулами Крамера: . 2. Если , а хотя бы один из отличен от нуля, то система не имеет решений. 3.Если все определители ,, то в случае: а)неравенства ранга основной матрицы системы рангу расширенной матрицы система не имеет решений; б)равенства ранга основной матрицы системы рангу расширенной матрицы, система имеет бесчисленное множество решений.